题目内容
18.探究题:某同学解方程组$\left\{\begin{array}{l}{\frac{1}{x+y}-\frac{1}{x-y}=\frac{1}{6}}\\{\frac{3}{x+y}+\frac{4}{x-y}=\frac{17}{6}}\end{array}\right.$,如下:解:设$\frac{1}{x+y}$=A,$\frac{1}{x-y}$=B,则原方程组变化为$\left\{\begin{array}{l}{A-B=\frac{1}{6}}\\{3A+4B=\frac{17}{6}}\end{array}\right.$,解得$\left\{\begin{array}{l}{A=\frac{1}{2}}\\{B=\frac{1}{3}}\end{array}\right.$.∴$\left\{\begin{array}{l}{x+y=2}\\{x-y=3}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=\frac{5}{2}}\\{y=-\frac{1}{2}}\end{array}\right.$.(1)你认为他的解答对吗?运用了换元思想方法.
(2)请你模仿他的解题方法,解方程组$\left\{\begin{array}{l}{\frac{2}{x+y}+\frac{3}{x-y}=2}\\{\frac{3}{x+y}-\frac{2}{x-y}=\frac{5}{6}}\end{array}\right.$.
分析 (1)运用了换元的思想方法;
(2)设$\frac{1}{x+y}$=m,$\frac{1}{x-y}$=n,解关于m、n的二元一次方程组,继而得关于x、y的方程组,求解可得.
解答 解:(1)他的解答对,运用了换元的思想方法;
(2)设$\frac{1}{x+y}$=m,$\frac{1}{x-y}$=n,
则原方程组变化为:$\left\{\begin{array}{l}{2m+3n=2}\\{3m-2n=\frac{5}{6}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=\frac{1}{2}}\\{n=\frac{1}{3}}\end{array}\right.$,
∴$\left\{\begin{array}{l}{x+y=2}\\{x-y=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=\frac{5}{2}}\\{y=-\frac{1}{2}}\end{array}\right.$.
故答案为:(1)换元.
点评 本题考查了解方程组的能力及换元的思想方法,准确而又简便换元是解题的关键,加减或代入法正确解方程组是解题的基础.

练习册系列答案
相关题目
6.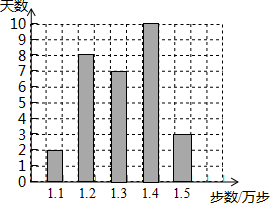 李阿姨是一名健步走运动的爱好者,她用手机软件记录了某个月(30天)每天健步走的步数(单位:万步),将记录结果绘制成如图所示的统计图,在每天所走的步数这组数据中,众数和中位数分别是( )
李阿姨是一名健步走运动的爱好者,她用手机软件记录了某个月(30天)每天健步走的步数(单位:万步),将记录结果绘制成如图所示的统计图,在每天所走的步数这组数据中,众数和中位数分别是( )
 李阿姨是一名健步走运动的爱好者,她用手机软件记录了某个月(30天)每天健步走的步数(单位:万步),将记录结果绘制成如图所示的统计图,在每天所走的步数这组数据中,众数和中位数分别是( )
李阿姨是一名健步走运动的爱好者,她用手机软件记录了某个月(30天)每天健步走的步数(单位:万步),将记录结果绘制成如图所示的统计图,在每天所走的步数这组数据中,众数和中位数分别是( )| A. | 1.2,1.3 | B. | 1.4,1.3 | C. | 1.4,1.35 | D. | 1.3,1.3 |
13.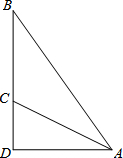 如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3$\sqrt{5}$米,坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带相连,若AB=10米,则旗杆BC的高为( )
如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3$\sqrt{5}$米,坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带相连,若AB=10米,则旗杆BC的高为( )
 如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3$\sqrt{5}$米,坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带相连,若AB=10米,则旗杆BC的高为( )
如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3$\sqrt{5}$米,坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带相连,若AB=10米,则旗杆BC的高为( )| A. | (3+$\sqrt{5}$)米 | B. | 8米 | C. | 6米 | D. | 5米 |
7.已知函数y=$\sqrt{x+1}$,则自变量x的取值范围是( )
| A. | x<-1 | B. | x>-1 | C. | x≤-1 | D. | x≥-1 |
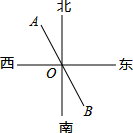 如图,已知点A、O、B在同一条直线上,若OA的方向是北偏西28°,则OB的方向是南偏东28°.
如图,已知点A、O、B在同一条直线上,若OA的方向是北偏西28°,则OB的方向是南偏东28°. 如图,边长为2的菱形ABCD中,BD=2,E、F分别是AD,CD上的动点(包含端点),且AE+CF=2,则线段EF长的取值范围是$\sqrt{3}$≤EF≤2.
如图,边长为2的菱形ABCD中,BD=2,E、F分别是AD,CD上的动点(包含端点),且AE+CF=2,则线段EF长的取值范围是$\sqrt{3}$≤EF≤2.
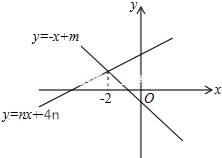 如图,直线y1=-x+m与y2=nx+4n(n≠0)的交点的横坐标为-2,图象可得关于x的不等式组$\left\{\begin{array}{l}{-x+m>nx+4n}\\{nx+4n>0}\end{array}\right.$的解集为-4<x<-2.
如图,直线y1=-x+m与y2=nx+4n(n≠0)的交点的横坐标为-2,图象可得关于x的不等式组$\left\{\begin{array}{l}{-x+m>nx+4n}\\{nx+4n>0}\end{array}\right.$的解集为-4<x<-2.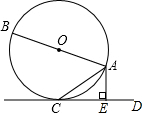 已知:如图,AB是⊙O的直径,CD是⊙O的切线,C为切点,AE⊥CD于E,求证:AC2=AE•AB.
已知:如图,AB是⊙O的直径,CD是⊙O的切线,C为切点,AE⊥CD于E,求证:AC2=AE•AB.