题目内容
13.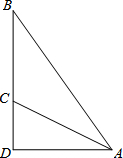 如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3$\sqrt{5}$米,坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带相连,若AB=10米,则旗杆BC的高为( )
如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3$\sqrt{5}$米,坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带相连,若AB=10米,则旗杆BC的高为( )| A. | (3+$\sqrt{5}$)米 | B. | 8米 | C. | 6米 | D. | 5米 |
分析 要求旗杆BC的高度,就要知道BC和CD的高度,就要先求出AD的长度.根据BC=BD-CD,即可得出结果.
解答 解:在Rt△ADC中,AC=3$\sqrt{5}$,由坡度为1:2,
∴CD=AC•sin∠ADC=3$\sqrt{5}$×$\frac{\sqrt{5}}{5}$=3,
AD=AC•cos∠ADC=3$\sqrt{5}$×$\frac{2\sqrt{5}}{5}$=6.
在Rt△ABD中,BD=$\sqrt{A{B}^{2}-A{E}^{2}}=\sqrt{1{0}^{2}-{6}^{2}}=8$.
∵BD=BC+CD,
∴BC=BD-CD=8-3=5(米).
答:旗杆的高度为5米.
故选D.
点评 本题考查了解直角三角形的应用-坡度坡角问题.两个直角三角形有公共的直角边,先求出公共边的长是解决此类题目的基本出发点.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
4.下列各组数中,以它们为边长的线段不能构成直角三角形的是( )
| A. | 1,$\sqrt{2}$,$\sqrt{3}$ | B. | 2,3,$\sqrt{6}$ | C. | 5,12,13 | D. | $\frac{5}{4}$,1,$\frac{3}{4}$ |
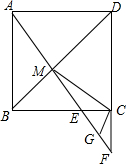 如图,正方形ABCD中,点E是BC上一点,直线AE交BD于点M,交DC的延长线于点F,G是EF的中点,连结CG.求证:
如图,正方形ABCD中,点E是BC上一点,直线AE交BD于点M,交DC的延长线于点F,G是EF的中点,连结CG.求证: