题目内容
10.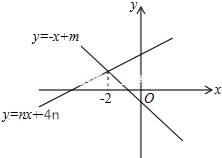 如图,直线y1=-x+m与y2=nx+4n(n≠0)的交点的横坐标为-2,图象可得关于x的不等式组$\left\{\begin{array}{l}{-x+m>nx+4n}\\{nx+4n>0}\end{array}\right.$的解集为-4<x<-2.
如图,直线y1=-x+m与y2=nx+4n(n≠0)的交点的横坐标为-2,图象可得关于x的不等式组$\left\{\begin{array}{l}{-x+m>nx+4n}\\{nx+4n>0}\end{array}\right.$的解集为-4<x<-2.
分析 满足不等式组$\left\{\begin{array}{l}{-x+m>nx+4n}\\{nx+4n>0}\end{array}\right.$就是直线y=-x+m位于直线y=nx+4n的上方且位于x轴的上方的图象,据此求得自变量的取值范围即可.
解答 解:∵直线y=-x+m与y=nx+4n(n≠0)的交点的横坐标为-2,
∴关于x的不等式-x+m>nx+4n的解集为x<-2,
∵y=nx+4n=0时,x=-4,
∴nx+4n>0的解集是x>-4,
∴不等式组$\left\{\begin{array}{l}{-x+m>nx+4n}\\{nx+4n>0}\end{array}\right.$的解集是-4<x<-2,
故答案为-4<x<-2.
点评 本题考查了一次函数的图象和性质以及与一元一次不等式的关系,要熟练掌握.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 如图,在正方形ABCD中,BD为一条对角线,点P为CD边上一点,A连接AP,并将△ADP平移使AD与BC边重合,P点落在DC的延长线上的一点G处,过G点作GH⊥BD于点H,连接HP和HC
如图,在正方形ABCD中,BD为一条对角线,点P为CD边上一点,A连接AP,并将△ADP平移使AD与BC边重合,P点落在DC的延长线上的一点G处,过G点作GH⊥BD于点H,连接HP和HC
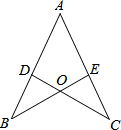 如图所示,在△ABC中,AB=AC,D、E是AB、AC的中点,求证:△ABE≌△ACD.
如图所示,在△ABC中,AB=AC,D、E是AB、AC的中点,求证:△ABE≌△ACD.