题目内容
9. 如图,边长为2的菱形ABCD中,BD=2,E、F分别是AD,CD上的动点(包含端点),且AE+CF=2,则线段EF长的取值范围是$\sqrt{3}$≤EF≤2.
如图,边长为2的菱形ABCD中,BD=2,E、F分别是AD,CD上的动点(包含端点),且AE+CF=2,则线段EF长的取值范围是$\sqrt{3}$≤EF≤2.
分析 由在边长为2的菱形ABCD中,BD=2,易得△ABD、△CBD都是边长为2的正三角形,继而证得△BDE≌△BCF(SAS),继而证得△BEF是正三角形,继而可得当动点E运动到点D或点A时,BE的最大,当BE⊥AD,即E为AD的中点时,BE的最小.
解答 解:∵四边形ABCD是边长为2的菱形,BD=2,
∴△ABD、△CBD都是边长为2的正三角形,
∵AE+CF=2,
∴CF=2-AE=AD-AE=DE,
又∵BD=BC=2,∠BDE=∠C=60°,
在△BDE和△BCF中,
$\left\{\begin{array}{l}{DE=DF}\\{∠BDE=∠C}\\{BD=BC}\end{array}\right.$,
∴△BDE≌△BCF(SAS),
∴∠EBD=∠FBC,
∴∠EBD+∠DBF=∠FBC+∠DBF,
∴∠EBF=∠DBC=60°,
又∵BE=BF,
∴△BEF是正三角形,
∴EF=BE=BF,
当动点E运动到点D或点A时,BE的最大值为2,
当BE⊥AD,即E为AD的中点时,BE的最小值为$\sqrt{3}$,
∵EF=BE,
∴EF的最大值为2,最小值为$\sqrt{3}$.
∴线段EF长的取值范围是:$\sqrt{3}$≤EF≤2.
故答案为:$\sqrt{3}$≤EF≤2.
点评 此题考查了菱形的性质、等边三角形的判定与性质以及全等三角形的判定与性质.注意证得△BDE≌△BCF是解此题的关键.

练习册系列答案
相关题目
19.若等腰三角形的底角为40°,则它的顶角度数为( )
| A. | 40° | B. | 100° | C. | 80° | D. | 70° |
17.已知两点A(4,6),B(6,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD,则点A的对应点C的坐标为( )
| A. | (2,3) | B. | (3,1) | C. | (2,1) | D. | (3,3) |
4.下列各组数中,以它们为边长的线段不能构成直角三角形的是( )
| A. | 1,$\sqrt{2}$,$\sqrt{3}$ | B. | 2,3,$\sqrt{6}$ | C. | 5,12,13 | D. | $\frac{5}{4}$,1,$\frac{3}{4}$ |
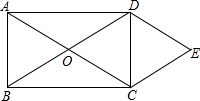 如图,已知O为矩形ABCD对角线的交点,过点D作DE∥AC,过点C作CE∥BD,且DE、CE相交于E点.
如图,已知O为矩形ABCD对角线的交点,过点D作DE∥AC,过点C作CE∥BD,且DE、CE相交于E点.