题目内容
5.在平面直角坐标系中,以方程组$\left\{\begin{array}{l}{y=x+1}\\{y=-x+1}\end{array}\right.$的解为坐标的点(x,y)到原点的距离为( )| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | -1 |
分析 此题中两方程未知数的系数较小,且对应的未知数的系数相等或互为相反数,所以可先用加减消元法再用代入消元法求出方程组的解.
解答 解:$\left\{\begin{array}{l}{y=x+1①}\\{y=-x+1②}\end{array}\right.$,
①+②得:2y=2,
解得y=1.
把y=1代入①得:x=0.
则点(0,2)到原点的距离为2.
故选:B.
点评 本题考查的是解二元一次方程组的加减消元法和代入消元法,及平面直角坐标系中各象限内点的坐标特点,需同学们熟练掌握.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20. 如图,直线m∥n,∠1=70°,∠2=30°,则∠A等于( )
如图,直线m∥n,∠1=70°,∠2=30°,则∠A等于( )
 如图,直线m∥n,∠1=70°,∠2=30°,则∠A等于( )
如图,直线m∥n,∠1=70°,∠2=30°,则∠A等于( )| A. | 30° | B. | 35° | C. | 40° | D. | 50° |
5. 如图所示,将纸片△ABC沿着DE折叠压平,则( )
如图所示,将纸片△ABC沿着DE折叠压平,则( )
 如图所示,将纸片△ABC沿着DE折叠压平,则( )
如图所示,将纸片△ABC沿着DE折叠压平,则( )| A. | ∠A=∠1+∠2 | B. | ∠A=$\frac{1}{2}$(∠1+∠2) | C. | ∠A=$\frac{1}{3}$(∠1+∠2) | D. | ∠A=$\frac{1}{4}$(∠1+∠2) |
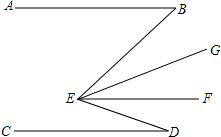 如图,AB∥EF∥CD,EG平分∠BEF,∠B+∠BED+∠D=192°,∠B-∠D=24°,则∠GEF=30°.
如图,AB∥EF∥CD,EG平分∠BEF,∠B+∠BED+∠D=192°,∠B-∠D=24°,则∠GEF=30°.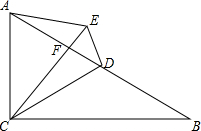 如图,在△ABC中,∠ACB=90°,∠B=30°,且点D是AB的中点,E为△ABC外一点,连接AE、DE,连接CE交AB于F,且∠CAD=∠CED.
如图,在△ABC中,∠ACB=90°,∠B=30°,且点D是AB的中点,E为△ABC外一点,连接AE、DE,连接CE交AB于F,且∠CAD=∠CED. 如图,已知直线AB∥DE.
如图,已知直线AB∥DE.