题目内容
10. 如图,已知直线AB∥DE.
如图,已知直线AB∥DE.(1)当∠B=27°,∠D=123°时,求∠DCB的大小;
(2)写出∠B,∠DCB,∠D之间的数量关系,不必说明理由.
分析 (1)首先过点C作CF∥AB,由平行线的性质:两直线平行,内错角相等,即可求得答案;
(2)根据(1)的结论解答即可.
解答 解:(1)过点C作CF∥AB,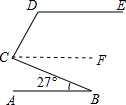
∵CF∥AB,
∴∠FCB=∠B=27°,
∵CF∥AB,AB∥DE.
∴CF∥DE,
∴∠DCF=180°-∠D=57°,
∴∠DCB=∠FCB+∠DCF=84°;
(2)∠DCB-∠B+∠D=180°,
∵CF∥AB,AB∥DE,CF∥DE,
∴∠FCB=∠B,∠DCF=180°-∠D,
∵∠DCB=∠FCB+∠DCF,
∴∠DCB-∠B+∠D=180°.
点评 此题考查了平行线的性质.此题比较简单,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.在平面直角坐标系中,以方程组$\left\{\begin{array}{l}{y=x+1}\\{y=-x+1}\end{array}\right.$的解为坐标的点(x,y)到原点的距离为( )
| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | -1 |
19. 如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,AD=6,AB=8,则$\frac{AF}{FC}$=( )
如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,AD=6,AB=8,则$\frac{AF}{FC}$=( )
 如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,AD=6,AB=8,则$\frac{AF}{FC}$=( )
如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,AD=6,AB=8,则$\frac{AF}{FC}$=( )| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{2}$ | D. | $\frac{2}{3}$ |
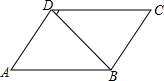 已知:平行四边形ABCD,BD为对角线(如图)∠A=70°,∠BDC=30°,AD=15.求:∠C,∠ADB的度数,并求BC边的长.
已知:平行四边形ABCD,BD为对角线(如图)∠A=70°,∠BDC=30°,AD=15.求:∠C,∠ADB的度数,并求BC边的长.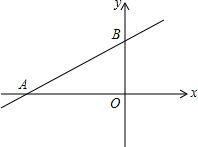 一次函数y=$\frac{\sqrt{3}}{3}$x+3的图象分别交x、y轴于A、B两点,是否在坐标轴上存在一点C使得△ABC为直角三角形?若有,请求出C点的坐标.
一次函数y=$\frac{\sqrt{3}}{3}$x+3的图象分别交x、y轴于A、B两点,是否在坐标轴上存在一点C使得△ABC为直角三角形?若有,请求出C点的坐标.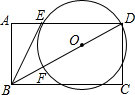 如图,在矩形ABCD中,点O在对角线BD上,以OD的长为半径的⊙O与AD、BD分别交于点E、F,且∠ABE=∠DBC.
如图,在矩形ABCD中,点O在对角线BD上,以OD的长为半径的⊙O与AD、BD分别交于点E、F,且∠ABE=∠DBC.