题目内容
15.若等腰三角形三边长均为整数,周长是11,则满足条件的三角形有3个.分析 已知等腰三角形的周长,求三边,则需要列出所有的组合形式,然后根据三角形的构造条件判断哪些符合,即可求得答案.
解答 解:等腰三角形的三边均为整数且它的周长为11,那三边的组合方式有以下几种:
①1,1,9;②2,2,7;③3,3,5;④4,4,3;⑤5,5,1;
又因为三角形两边之和大于第三边,两边之差小于第三边,则③④⑤符合,
所以满足条件的三角形有3个.
故答案为:3.
点评 本题考查了等腰三角形的性质和三角形的三边关系;已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形进行解答,这点非常重要,也是解题的关键;其中三边为整数也是非常重要的条件.

练习册系列答案
相关题目
6.已知空气的单位体积质量为1,29×10-3克/厘米3,1.29×10-3用小数表示为( )
| A. | 0.00129 | B. | 0.0129 | C. | -0.00129 | D. | 0.000129 |
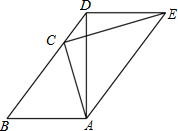 如图,在△ABC中,AB=AC,作AD⊥AB交BC的延长线于点D,作CE⊥AC,且使AE∥BD,连结DE.
如图,在△ABC中,AB=AC,作AD⊥AB交BC的延长线于点D,作CE⊥AC,且使AE∥BD,连结DE. 如图,矩形OABC的顶点A、C的坐标分别为(0,10)、(4,0),反比例函数y=$\frac{k}{x}(k≠0)$在第一象限内的图象过矩形OABC的对角线的交点M,并与AB、BC分别交于点E、F,连接OE、EF、OF,则△OEF的面积为$\frac{75}{4}$.
如图,矩形OABC的顶点A、C的坐标分别为(0,10)、(4,0),反比例函数y=$\frac{k}{x}(k≠0)$在第一象限内的图象过矩形OABC的对角线的交点M,并与AB、BC分别交于点E、F,连接OE、EF、OF,则△OEF的面积为$\frac{75}{4}$. 如图,三个全等的小矩形沿“横-竖-横”排列在一个边长分别为5.7,4.5的大矩形中,图中一个小矩形的周长等于6.8.
如图,三个全等的小矩形沿“横-竖-横”排列在一个边长分别为5.7,4.5的大矩形中,图中一个小矩形的周长等于6.8.