题目内容
9.已知关于x,y的二元一次方程组$\left\{\begin{array}{l}{3x-ay=5}\\{x+by=11}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=5}\\{y=6}\end{array}\right.$,那么关于x,y的二元一次方程组$\left\{\begin{array}{l}{3(x+y)-a(x-y)=5}\\{x+y+b(x-y)=11}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=\frac{11}{2}}\\{y=-\frac{1}{2}}\end{array}\right.$.分析 法1:把已知方程组的解代入方程求出a与b的值,代入所求方程组求出解即可;
法2:根据已知方程组的解列出关于x与y的方程组,求出解即可.
解答 解:法1:把$\left\{\begin{array}{l}{x=5}\\{y=6}\end{array}\right.$代入已知方程组得:$\left\{\begin{array}{l}{15-6a=5}\\{5+6b=11}\end{array}\right.$,
解得:a=$\frac{5}{3}$,b=1,
代入所求方程组,整理得:$\left\{\begin{array}{l}{4x+14y=15①}\\{2x=11②}\end{array}\right.$,
由②得:x=$\frac{11}{2}$,
把x=$\frac{11}{2}$代入①得:y=-$\frac{1}{2}$,
则方程组的解为$\left\{\begin{array}{l}{x=\frac{11}{2}}\\{y=-\frac{1}{2}}\end{array}\right.$;
法2:由已知方程组的解得到$\left\{\begin{array}{l}{x+y=5}\\{x-y=6}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=\frac{11}{2}}\\{y=-\frac{1}{2}}\end{array}\right.$.
故答案为:$\left\{\begin{array}{l}x=\frac{11}{2}\\ y=-\frac{1}{2}\end{array}\right.$.
点评 此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程都成立的未知数的值.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
1.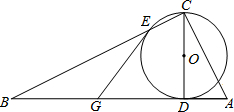 已知CD为Rt△ABC斜边AB上的高,以CD为直径的圆交BC于E点,交AC于F点,G为BD的中点.
已知CD为Rt△ABC斜边AB上的高,以CD为直径的圆交BC于E点,交AC于F点,G为BD的中点.
(1)求证:GE为⊙O的切线;
(2)若tanB=$\frac{1}{2}$,GE=5,求AD的长.
 已知CD为Rt△ABC斜边AB上的高,以CD为直径的圆交BC于E点,交AC于F点,G为BD的中点.
已知CD为Rt△ABC斜边AB上的高,以CD为直径的圆交BC于E点,交AC于F点,G为BD的中点.(1)求证:GE为⊙O的切线;
(2)若tanB=$\frac{1}{2}$,GE=5,求AD的长.
16.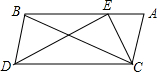 如图,E为△ABC中AB边上一点,△ABC≌△EDC,∠ACE=46°,则∠DEB+∠BDC=( )
如图,E为△ABC中AB边上一点,△ABC≌△EDC,∠ACE=46°,则∠DEB+∠BDC=( )
 如图,E为△ABC中AB边上一点,△ABC≌△EDC,∠ACE=46°,则∠DEB+∠BDC=( )
如图,E为△ABC中AB边上一点,△ABC≌△EDC,∠ACE=46°,则∠DEB+∠BDC=( )| A. | 107° | B. | 113° | C. | 115° | D. | 117° |
 如图,⊙O的半径为5,正五边形ABCDE内接于⊙O,则$\widehat{AB}$的长度为2π.
如图,⊙O的半径为5,正五边形ABCDE内接于⊙O,则$\widehat{AB}$的长度为2π. 在“世界粮食日”前夕,某校团委随机抽取了n名本校学生,对某日午餐剩饭菜情况进行问卷调查.问卷中的剩饭菜情况包括:
在“世界粮食日”前夕,某校团委随机抽取了n名本校学生,对某日午餐剩饭菜情况进行问卷调查.问卷中的剩饭菜情况包括: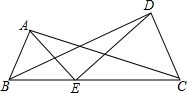 如图,E是线段BC上的一点,A,D是BC同侧的两点,∠AEB=∠DEC,∠ACB=∠BDE,DE=CE,试证明AE=BE.有一位同学是这样思考的:
如图,E是线段BC上的一点,A,D是BC同侧的两点,∠AEB=∠DEC,∠ACB=∠BDE,DE=CE,试证明AE=BE.有一位同学是这样思考的: