题目内容
14.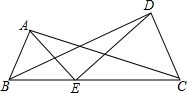 如图,E是线段BC上的一点,A,D是BC同侧的两点,∠AEB=∠DEC,∠ACB=∠BDE,DE=CE,试证明AE=BE.有一位同学是这样思考的:
如图,E是线段BC上的一点,A,D是BC同侧的两点,∠AEB=∠DEC,∠ACB=∠BDE,DE=CE,试证明AE=BE.有一位同学是这样思考的:∠AEB=∠DEC$\stackrel{①}{→}$∠AEB+∠AED=∠DEC+∠AED$\stackrel{②}{→}$$\left.\begin{array}{l}{∠BED=∠AEC}\\{DE=CE}\\{∠BDE=∠ACE}\end{array}\right\}$$\stackrel{③}{→}$△BED≌△AEC$\stackrel{④}{→}$AE=BE
请你写出每一步的理由.
①已知;
②等式性质;
③角的和差定义;
④ASA.
分析 根据两角夹边对应相等的两个三角形全等可以证明,写出理由即可.
解答 证明:∵ ∠AEB=∠DEC(①已知),
∠AEB=∠DEC(①已知),
∴∠AEB+∠AED=∠DEC+∠AED(②等式性质),
∴∠BED=∠AEC(③角的和差定义),
在△BED和△AEC中,
$\left\{\begin{array}{l}{∠BED=∠AEC}\\{DE=CE}\\{∠BDE=∠ACE}\end{array}\right.$,
∴△BED≌△AEC(④ASA),
∴AE=BE.
故答案分别为已知,等式性质,角的和差定义,ASA.
点评 本题考查全等三角形的判定和性质,解题的关键是熟练掌握全等三角形的判定和性质,属于基础题,中考常考题型.

练习册系列答案
相关题目
19.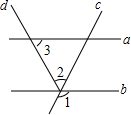 如图,a∥b,∠1=110°,∠3=40°,则∠2等于( )
如图,a∥b,∠1=110°,∠3=40°,则∠2等于( )
 如图,a∥b,∠1=110°,∠3=40°,则∠2等于( )
如图,a∥b,∠1=110°,∠3=40°,则∠2等于( )| A. | 40° | B. | 60° | C. | 70° | D. | 80° |
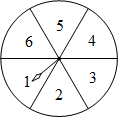 如图,转盘被等分成6个扇形,每个扇形上依次标有数字1,2,3,4,5,6.在游戏中特别规定:当指针指向边界时,重新转动转盘.
如图,转盘被等分成6个扇形,每个扇形上依次标有数字1,2,3,4,5,6.在游戏中特别规定:当指针指向边界时,重新转动转盘.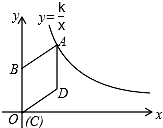 如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=$\frac{k}{x}$(x>0)的图象上,点D的坐标为(4,3).
如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=$\frac{k}{x}$(x>0)的图象上,点D的坐标为(4,3).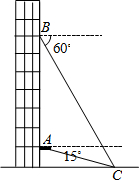 从一幢建筑大楼的两个观察点A,B观察地面的花坛(点C),测得俯角分别为15°和60°,如图,直线AB与地面垂直,AB=50米,试求出点B到点C的距离.(结果保留根号)
从一幢建筑大楼的两个观察点A,B观察地面的花坛(点C),测得俯角分别为15°和60°,如图,直线AB与地面垂直,AB=50米,试求出点B到点C的距离.(结果保留根号)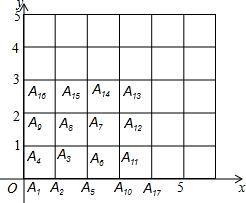 如图所示,已知点A1的坐标为(0,0),点A2的坐标为(1,0),点A3的坐标为(1,1),点A4的坐标为(0,1),A5的坐标为(2,0),点A6坐标为(2,1),点A7的坐标为(2,2),点A8的坐标为(1,2),点A9的坐标为(0,2),点A10的坐标为(3,0),点A11的坐标为(3,1),…,依此规律排列下去,则点A25的坐标为(0,4),点A2015的坐标为(34,44).
如图所示,已知点A1的坐标为(0,0),点A2的坐标为(1,0),点A3的坐标为(1,1),点A4的坐标为(0,1),A5的坐标为(2,0),点A6坐标为(2,1),点A7的坐标为(2,2),点A8的坐标为(1,2),点A9的坐标为(0,2),点A10的坐标为(3,0),点A11的坐标为(3,1),…,依此规律排列下去,则点A25的坐标为(0,4),点A2015的坐标为(34,44).