题目内容
1.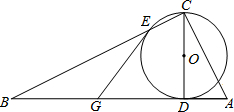 已知CD为Rt△ABC斜边AB上的高,以CD为直径的圆交BC于E点,交AC于F点,G为BD的中点.
已知CD为Rt△ABC斜边AB上的高,以CD为直径的圆交BC于E点,交AC于F点,G为BD的中点.(1)求证:GE为⊙O的切线;
(2)若tanB=$\frac{1}{2}$,GE=5,求AD的长.
分析 (1)连DE、OE,利用圆周角定理可得∠CED=∠BED=90°,因为G为BD的中点,由直角三角形的性质可得GE=GD,再由OE=OD,易得∠OED=∠ODE,可得∠GEO=∠GDO,由CD⊥AB,可得∠GEO=∠GDO=90°,可得结论;
(2)首先由垂直的定义易得∠B=∠ACD,利用锐角三角函数可得tanB=$\frac{1}{2}$=$\frac{CD}{BD}$=tan∠DCA=$\frac{AD}{CD}$=$\frac{1}{2}$,易得BD=4AD,可得结果.
解答 (1)证明:连DE、OE,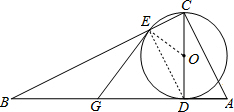
∵CD为⊙O的直径,
∴∠CED=∠BED=90°,
∵G为BD的中点,
∴GE=GD,
∴GED=∠GDE,
∵OE=OD,
∴∠OED=∠ODE,
∴∠GEO=∠GDO,
∴CD⊥AB,
∴∠GEO=∠GDO=90°,
∴GE为⊙O的切线;
(2)∵CD⊥AB,
∴∠ACD=90°-∠A,
∵∠BCA=90°,
∴∠B=90°-∠A,
∴∠B=∠ACD,
∵tanB=$\frac{1}{2}$=$\frac{CD}{BD}$=tan∠DCA=$\frac{AD}{CD}$=$\frac{1}{2}$,
∴BD=4AD,
∵EG=5,
∴BD=10,AD=$\frac{5}{2}$.
点评 本题主要考查了切线的判定及锐角三角函数等,作出恰当的辅助线是解答此题的关键.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
11.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
12.使得二次根式$\sqrt{3-4x}$有意义的字母x的取值范围是( )
| A. | x≥$\frac{3}{4}$ | B. | x≤$\frac{3}{4}$ | C. | x<$\frac{3}{4}$ | D. | x≠$\frac{3}{4}$ |
8.关于x的分式方程$\frac{3}{x}$+$\frac{6}{x-1}$-$\frac{x+k}{x(x-1)}$=0有解,则k满足( )
| A. | k≠-3 | B. | k≠5 | C. | k≠-3且k≠-5 | D. | k≠-3且k≠5 |

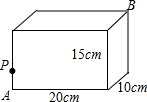 如图,长方体的长为20cm,宽为10cm,高为15cm,棱上点P与顶点A相距5cm,一只蚂蚁如果要沿着长方体表面从点P爬到点B处,需要爬行的最短距离是多少?
如图,长方体的长为20cm,宽为10cm,高为15cm,棱上点P与顶点A相距5cm,一只蚂蚁如果要沿着长方体表面从点P爬到点B处,需要爬行的最短距离是多少?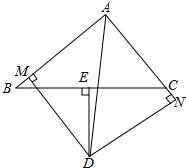 如图,△ABC中,E是BC边上的中点,DE⊥BC于E,交∠BAC的平分线AD于D,过D点作DM⊥AB于M,作DN⊥AC于N,试证明:BM=CN.
如图,△ABC中,E是BC边上的中点,DE⊥BC于E,交∠BAC的平分线AD于D,过D点作DM⊥AB于M,作DN⊥AC于N,试证明:BM=CN.