题目内容
5.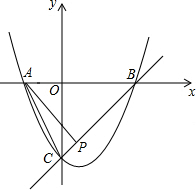 如图,已知抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于点C,O是坐标原点,点A的坐标是(-1,0),点C的坐标是(0,-3)
如图,已知抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于点C,O是坐标原点,点A的坐标是(-1,0),点C的坐标是(0,-3)(1)求抛物线的函数表达式;
(2)求直线BC的函数表达式;
(3)P为线段BC上一点,连接AC,AP,若∠ACB=∠PAB,求△PAB的面积.
分析 (1)根据待定系数法,可得函数解析式;
(2)根据自变量与函数值的对应关系,可得B点坐标,根据待定系数法,可得函数解析式;
(3)根据两个角对应相等的两个三角形相似,相思三角形的性质,可得BP的长,再根据平行线截三角形所得的三角形相似,相似三角形的性质,可得BD的长,根据三角形的面积公式,可得答案.
解答 解:(1)将A、C点坐标代入函数解析式,得
$\left\{\begin{array}{l}{1-b+c=0}\\{c=-3}\end{array}\right.$,解得$\left\{\begin{array}{l}{b=-2}\\{c=-3}\end{array}\right.$,
抛物线的解析式为y=x2-2x-3;
(2)当y=0时,x2-2x-3=0,解得x=-1(不符合题意,舍),x=3,即B点坐标为(3,0).
设直线BC的解析式为y=kx+b,将B、C点的坐标代入,得
$\left\{\begin{array}{l}{b=-3}\\{3k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=1}\\{b=-3}\end{array}\right.$,
直线BC的解析式为y=x-3;
(3)如图 ,
,
过点P作PD⊥x轴于点D,∵∠ACB=∠PAB,∠ABC=∠PBA,
∴△ABP∽△CBA,$\frac{AB}{BC}$=$\frac{BP}{AB}$.
∵BO=OC=3,
∴BC=3$\sqrt{2}$.
∵A(-1,0),B(3,0),
∴AB=4,∴$\frac{4}{3\sqrt{2}}$=$\frac{BP}{4}$,
解得BP=$\frac{8\sqrt{2}}{3}$.
由题意可得:PD∥OC,
∴△BDP∽△BOC,∴$\frac{PB}{BC}$=$\frac{DP}{CO}$=$\frac{BD}{BO}$,
则$\frac{\frac{8\sqrt{2}}{3}}{3\sqrt{2}}$=$\frac{DP}{3}$=$\frac{BD}{3}$,
解得DP=BD=$\frac{8}{3}$,
S△APB=$\frac{1}{2}$AB•PD=$\frac{1}{2}$×$\frac{8}{3}$×4=$\frac{16}{3}$.
点评 本题考查了二次函数综合题,利用待定系数法求函数解析式;利用相似三角形的判定与性质得出PD的长是解题关键.

 阅读快车系列答案
阅读快车系列答案2016年2月上旬福州地区空气质量指数(AQI)
| 日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| ug/m3 | 26 | 34 | 43 | 41 | 34 | 48 | 78 | 1 15 | 59 | 45 |
| A. | -1 | B. | -3 | C. | 3 | D. | 7 |
 如图,已知l1∥l2∥l3,DE=4,DF=6,那么下列结论正确的是( )
如图,已知l1∥l2∥l3,DE=4,DF=6,那么下列结论正确的是( )| A. | BC:EF=1:1 | B. | BC:AB=1:2 | C. | AD:CF=2:3 | D. | BE:CF=2:3 |
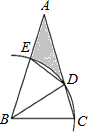 如图,△ABC中,∠A=30°,AB=AC,以B为圆心,BC长为半径画弧,交AC于点D,交AB于点E
如图,△ABC中,∠A=30°,AB=AC,以B为圆心,BC长为半径画弧,交AC于点D,交AB于点E