题目内容
17.(1)如图,在△ABC和△BAD中,AC与BD相交于点E,AD=BC,∠DAB=∠CBA.求证:AC=BD.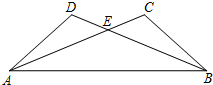
(2)如图,?ABCD中,AB=3,AD=5,∠BAD的平分线交BC于点E.求EC的长.
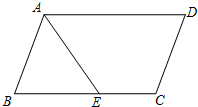
分析 (1)根据SAS证出△ABC≌△BAD,可直接得出AC=BD.
(2)根据平行四边形的性质得出AD=BC,∠DAE=∠BEA,再根据角平分线的性质得出∠BAE=∠DAE,从而得出∠BAE=∠BEA,即可得出BE=BA,再根据EC=BC-BE,求出EC的长.
解答 解:(1)在△ABC和△ABD中,
∵$\left\{\begin{array}{l}{AD=BC}\\{∠DAB=∠CBA}\\{AB=BA}\end{array}\right.$,
∴△ABC≌△BAD (SAS),
∴AC=BD.
(2)∵四边形ABCD是平行四边形,AB=3,BC=5,
∴AD∥BC,AD=BC=5,
∴∠DAE=∠BEA,
∵AE是∠BAD的平分线,
∴∠BAE=∠DAE,
∴∠BAE=∠BEA,
∴BE=BA=3,
∴EC=BC-BE=2.
点评 此题考查了全等三角形的判定与性质和平行四边的性质,用到的知识点是全等三角形的判定与性质、平行四边的性质、角平分线的定义、等边对等角、平行线的性质等,熟练掌握有关知识是本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.下列运算结果是a6的式子是( )
| A. | a2•a3 | B. | (-a)6 | C. | (a3)3 | D. | a12-a6 |
2.下列说法中,正确的是( )
| A. | 关于某条直线对称的两个三角形一定全等 | |
| B. | 两个全等三角形一定关于某条直线对称 | |
| C. | 面积相等的两个三角形一定关于某条直线之间对称 | |
| D. | 周长相等的两个三角形一定关于某条直线之间对称 |
6.下列关于x的方程一定有实数解的是( )
| A. | 2x=m | B. | x2=m | C. | $\frac{1}{x+1}$=m | D. | $\sqrt{x+1}$=m |
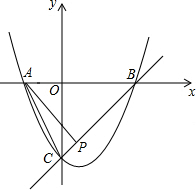 如图,已知抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于点C,O是坐标原点,点A的坐标是(-1,0),点C的坐标是(0,-3)
如图,已知抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于点C,O是坐标原点,点A的坐标是(-1,0),点C的坐标是(0,-3)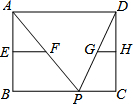 如图,矩形ABCD中,AD=10,点P为BC上任意一点,分别连接AP、DP,E、F、G、H分别为AB、AP、DP、DC的中点,则EF+GH的值为( )
如图,矩形ABCD中,AD=10,点P为BC上任意一点,分别连接AP、DP,E、F、G、H分别为AB、AP、DP、DC的中点,则EF+GH的值为( )