题目内容
20.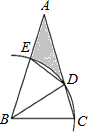 如图,△ABC中,∠A=30°,AB=AC,以B为圆心,BC长为半径画弧,交AC于点D,交AB于点E
如图,△ABC中,∠A=30°,AB=AC,以B为圆心,BC长为半径画弧,交AC于点D,交AB于点E(1)求∠ABD的度数;
(2)当BC=$\sqrt{2}$时,求线段AE,AD与$\widehat{DE}$围成阴影部分的面积.
分析 (1)根据AB=AC,利用三角形内角和定理求出∠ABC、∠BCD的度数,再利用等腰三角形的性质和三角形内角和定理求出∠DBC=30°,然后即可求出∠ABD的度数;
(2)过点D作DF⊥AB与F,在RT△BDF中和RT△BDF中分别求出DF、BF、AF的长,即可知AB的长,最后根据S阴影=S△ABD-S扇形BDE列式可求得.
解答 解:(1)∵AB=AC,∠A=30°,
∴∠ABC=∠ACB=75°,
∵BC=BD,
∴∠BDC=∠BCD=75°,
∴∠DBC=30°,
∴∠ABD=∠ABC-∠DBC=45°;
(2)过点D作DF⊥AB与F,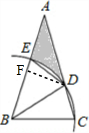
在RT△BDF中,∠FBD=45°,BD=BC=$\sqrt{2}$,
∴BF=DF=BDsin45°=$\sqrt{2}$×$\frac{\sqrt{2}}{2}$=1,
在RT△BDF中,∠A=30°,
∴AD=2DF=2,AF=$\sqrt{3}$,
∴AB=AF+BF=$\sqrt{3}$+1,
∴S阴影=S△ABD-S扇形BDE
=$\frac{1}{2}$AB•DF-$\frac{45}{360}•π•(\sqrt{2})^{2}$
=$\frac{\sqrt{3}+1}{2}-\frac{π}{4}$.
点评 本题主要考查对等腰三角形的性质和扇形面积等知识点的理解和掌握,此题的突破点是利用等腰三角形的性质和三角形内角和定理求出∠DBC=30°,然后利用割补法可求阴影部分面积.

练习册系列答案
相关题目
10.为了了解某社区居民的用电情况,随机对该社区10户居民进行了调查,下表是这10户居民2014年4月份用电量的调查结果:
下列结论不正确的是( )
| 居民户数 | 1 | 3 | 2 | 4 |
| 月用电量(度/户) | 40 | 50 | 55 | 60 |
| A. | 众数是60 | B. | 平均数是54 | C. | 中位数是55 | D. | 方差是29 |
8.下列运算结果是a6的式子是( )
| A. | a2•a3 | B. | (-a)6 | C. | (a3)3 | D. | a12-a6 |
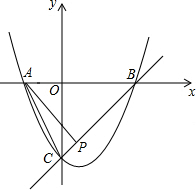 如图,已知抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于点C,O是坐标原点,点A的坐标是(-1,0),点C的坐标是(0,-3)
如图,已知抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于点C,O是坐标原点,点A的坐标是(-1,0),点C的坐标是(0,-3)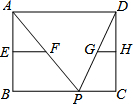 如图,矩形ABCD中,AD=10,点P为BC上任意一点,分别连接AP、DP,E、F、G、H分别为AB、AP、DP、DC的中点,则EF+GH的值为( )
如图,矩形ABCD中,AD=10,点P为BC上任意一点,分别连接AP、DP,E、F、G、H分别为AB、AP、DP、DC的中点,则EF+GH的值为( )