题目内容
13.课上教师呈现一个问题:已知:如图1,AB∥CD,EF⊥AB于点O,FG交CD于点P,当∠1=30°时,求∠EFG的度数.
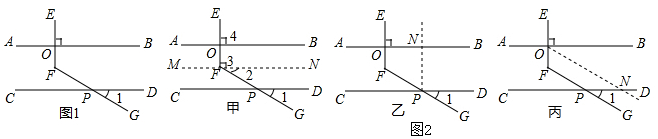
甲、乙、丙三位同学用不同的方法添加辅助线解决问题,如图2.
(1)甲同学辅助线的做法为过点F作MN∥CD,请根据甲同学作辅助线的方法求∠EFG的度数;
(2)乙同学辅助线的做法为过P作PN∥EF;丙同学辅助线的做法为过O作ON∥FG;
(3)请你任选乙同学或丙同学所描述辅助线的一种做法,求∠EFG的度数.
分析 (1)过F作MN∥CD,根据平行线的性质以及垂线的定义,即可得到∠EFG的度数;
(2)由图可得,乙同学辅助线的做法为过P作PN∥EF;丙同学辅助线的做法为过O作ON∥FG;
(3)若选择乙,过P作PN∥EF,根据平行线的性质,可得∠NPD的度数,再根据∠1的度数以及平行线的性质,即可得到∠EFG的度数;若选择丙,过O作ON∥FG,先根据平行线的性质,得到∠BON的度数,再根据平行线的性质以及垂线的定义,即可得到∠EFG的度数.
解答  解:(1)如图甲,过F作MN∥CD,
解:(1)如图甲,过F作MN∥CD,
∵MN∥CD,∠1=30°,
∴∠2=∠1=30°,
∵AB∥CD,
∴AB∥MN,
∵AB⊥EF,
∴∠3=∠4=90°,
∴∠EFG=∠3+∠2=90°+30°=120°.
(2)由图可得,乙同学辅助线的做法为过P作PN∥EF;丙同学辅助线的做法为过O作ON∥FG;
故答案为:过P作PN∥EF;过O作ON∥FG;
(3)若选择乙,理由如下:
如图乙,过P作PN∥EF,
∵PN∥EF,EF⊥AB,
∴∠ONP=∠ENB=90°,
∵AB∥CD,
∴∠NPD=∠ONP=90°,
又∵∠1=30°,
∴∠NPG=90°+30°=120°,
∵PN∥EF,
∴∠EFG=∠NPG=120°;
若选择丙,理由如下:
如图丙,过O作ON∥FG,
∵ON∥FG,∠1=30°,
∴∠PNO=∠1=30°,
∵AB∥CD,
∴∠BON=∠PNO=30°,
又∵EF⊥AB,
∴∠EON=∠EOB+∠BON=90°+30°=120°,
∵ON∥FG,
∴∠EFG=∠EON=120°.
点评 本题主要考查了平行线的性质的运用,解决问题的关键是作辅助线构造内错角或同位角,依据平行线的性质进行计算求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
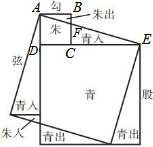 魏晋时期,伟大数学家刘徽利用如图通过“以盈补虚,出入相补”的方法,即“勾自乘为朱方,股自乘为青方,令出入相补,各从其类”证明了勾股定理,若图中BF=2,CF=4,则AE的长为6$\sqrt{10}$.
魏晋时期,伟大数学家刘徽利用如图通过“以盈补虚,出入相补”的方法,即“勾自乘为朱方,股自乘为青方,令出入相补,各从其类”证明了勾股定理,若图中BF=2,CF=4,则AE的长为6$\sqrt{10}$.