题目内容
18.解方程:$\frac{x}{x+2}$-$\frac{8}{{x}^{2}-4}$=1.分析 根据等式的性质,可得整式方程,根据解整式方程,可得答案.
解答 解:方程两边都乘以(x+2)(x-2),得
x(x-2)-8=x2-4,
解得x=-2,
经检验:x=-2是原方程的增根,
∴原方程无解.
点评 本题考查了解分式方程,利用等式的性质得出整式方程是解题关键.

练习册系列答案
相关题目
10.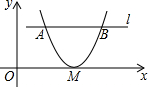 如图在平面直角坐标系中,抛物线y=(x-h)2与x轴只有一个交点M,与平行于x轴的直线l交于A,B两点.若AB=3,则点M到直线l的距离为( )
如图在平面直角坐标系中,抛物线y=(x-h)2与x轴只有一个交点M,与平行于x轴的直线l交于A,B两点.若AB=3,则点M到直线l的距离为( )
 如图在平面直角坐标系中,抛物线y=(x-h)2与x轴只有一个交点M,与平行于x轴的直线l交于A,B两点.若AB=3,则点M到直线l的距离为( )
如图在平面直角坐标系中,抛物线y=(x-h)2与x轴只有一个交点M,与平行于x轴的直线l交于A,B两点.若AB=3,则点M到直线l的距离为( )| A. | $\frac{5}{2}$ | B. | $\frac{9}{4}$ | C. | 2 | D. | $\frac{7}{4}$ |
8.利用一副三角板,能作出大于0°而小于90°的角共有( )
| A. | 13个 | B. | 11个 | C. | 5个 | D. | 4个 |
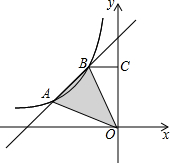 如图,直线y=x+4与双曲线y=$\frac{k}{x}$(x<0)交于点A、B,过点B向y轴作垂线,垂足为C,若BC=$\frac{1}{2}$AB,△AOB的面积为3,则k值为-3$\sqrt{2}$+$\frac{9}{8}$.
如图,直线y=x+4与双曲线y=$\frac{k}{x}$(x<0)交于点A、B,过点B向y轴作垂线,垂足为C,若BC=$\frac{1}{2}$AB,△AOB的面积为3,则k值为-3$\sqrt{2}$+$\frac{9}{8}$.
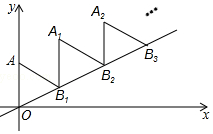 如图,放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为2的等边三角形,边AO在y轴上,点B1、B2、B3…都在直线y=$\frac{\sqrt{3}}{3}$x上,则点A2017的坐标为(2017$\sqrt{3}$,2019).
如图,放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为2的等边三角形,边AO在y轴上,点B1、B2、B3…都在直线y=$\frac{\sqrt{3}}{3}$x上,则点A2017的坐标为(2017$\sqrt{3}$,2019).