题目内容
16.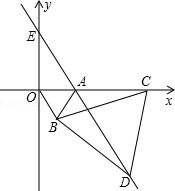 如图,直角坐标系中,点A的坐标为(1,0),以线段OA为边在第四象限内作等边△AOB,点C为x正半轴上一动点(OC>1),连接BC,以线段BC为边在第四象限内作等边△CBD,直线DA交y轴于点E.
如图,直角坐标系中,点A的坐标为(1,0),以线段OA为边在第四象限内作等边△AOB,点C为x正半轴上一动点(OC>1),连接BC,以线段BC为边在第四象限内作等边△CBD,直线DA交y轴于点E.①△OBC与△ABD全等吗?判断并证明你的结论;
②随着点C位置的变化,点E的位置是否会发生变化?若没有变化,求出点E的坐标;若有变化,请说明理由.
分析 ①先根据△AOB与△CBD均是等边三角形得出OB=AB,∠OBA=∠OAB=60°,BC=BD,∠CBD=60°,再由SAS定理即可得出结论;
②根据①容易得到∠OAE=60°,然后根据在Rt△OAE中30°的角所对的直角边等于斜边的一半可以得到AE=2,从而得到E的坐标是固定的.
解答 解:①全等.
理由:∵△AOB和△CBD是等边三角形,
∴OB=AB,∠OBA=∠OAB=60°,BC=BD,∠CBD=60°,
∴∠OBA+∠ABC=∠CBD+∠ABC,即∠OBC=∠ABD,
在△OBC和△ABD中,
∵$\left\{\begin{array}{l}OB=AB\\∠OBC=∠ABD\\ BC=BD\end{array}\right.$,
∴△OBC≌△ABD(SAS).
②不变.
理由:∵△OBC≌△ABD,
∴∠BAD=∠BOC=60°,
又∵∠OAB=60°,
∴∠OAE=180°-∠OAB-∠BAD=60°,
∴Rt△OEA中,AE=2OA=2,
∴OE=$\sqrt{3}$,
∴点E的位置不会发生变化,E的坐标为E(0,$\sqrt{3}$).
点评 本题考查的是一次函数综合题,涉及到等边三角形的性质、全等三角形的判定与性质等知识,难度适中.

练习册系列答案
相关题目
7.如图,在等腰Rt△ABC中,D为斜边AC边上一点,以CD为直角边,点C为直角顶点,向外构造等腰Rt△CDE.动点P从点A出发,以1个单位/s的速度,沿着折线A-D-E运动.在运动过程中,△BCP的面积S与运动时间t(s)的函数图象如图所示,则BC的长是( )
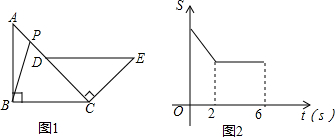

| A. | 2+$\sqrt{2}$ | B. | 4 | C. | 3$\sqrt{2}$ | D. | 2+2$\sqrt{2}$ |
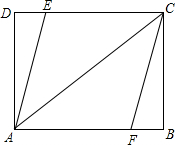 如图,矩形ABCD中,AB=8,AD=6,点E、F分别在边CD、AB上.
如图,矩形ABCD中,AB=8,AD=6,点E、F分别在边CD、AB上.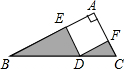 如图,Rt△ABC中,∠A=90°,四边形AEDF为正方形,E、D、F分别在Rt△ABC的三边上,BD=3,CD=2,则图中阴影部分的面积之和为3.
如图,Rt△ABC中,∠A=90°,四边形AEDF为正方形,E、D、F分别在Rt△ABC的三边上,BD=3,CD=2,则图中阴影部分的面积之和为3.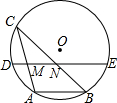 如图,⊙O的弦AB=4cm,点C为优弧$\widehat{AB}$上的动点,且∠ACB=30°.若弦DE经过弦AC、BC的中点M、N,则DM+EN的最大值是6cm.
如图,⊙O的弦AB=4cm,点C为优弧$\widehat{AB}$上的动点,且∠ACB=30°.若弦DE经过弦AC、BC的中点M、N,则DM+EN的最大值是6cm.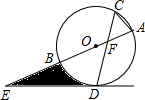 如图,⊙O的直径AB与弦CD相交于点F,且∠ACD=60°,在AB的延长线上取一点E,使得∠AED=30°.
如图,⊙O的直径AB与弦CD相交于点F,且∠ACD=60°,在AB的延长线上取一点E,使得∠AED=30°.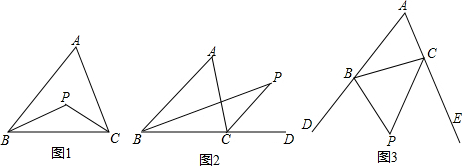
 如图用相同的小长方形壁砖铺满周长为500cm的大长方形电视机背景墙,求小长方形的长和宽.
如图用相同的小长方形壁砖铺满周长为500cm的大长方形电视机背景墙,求小长方形的长和宽.