题目内容
7.如图,在等腰Rt△ABC中,D为斜边AC边上一点,以CD为直角边,点C为直角顶点,向外构造等腰Rt△CDE.动点P从点A出发,以1个单位/s的速度,沿着折线A-D-E运动.在运动过程中,△BCP的面积S与运动时间t(s)的函数图象如图所示,则BC的长是( )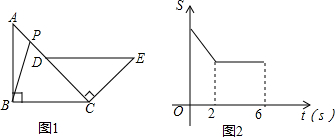
| A. | 2+$\sqrt{2}$ | B. | 4 | C. | 3$\sqrt{2}$ | D. | 2+2$\sqrt{2}$ |
分析 根据函数图象首先可求得AD=2,DE=4,然后利用特殊锐角三角函数值,可求得DC=2$\sqrt{2}$,从而得到AC=2+2$\sqrt{2}$,最后在Rt△ABC中可求得BC的长.
解答 解:根据题意可知:当点P在AP上运动时,三角形的面积不断减小,当点在DE上移动时,三角形的面积不变.
根据函数图象可知AD=2,DE=6-2=4.
在Rt△DEC中,$\frac{DC}{DE}=\frac{\sqrt{2}}{2}$,即$\frac{DC}{4}=\frac{\sqrt{2}}{2}$,
∴DC=2$\sqrt{2}$.
∴AC=AD+DC=2+2$\sqrt{2}$.
在Rt△ABC中,$\frac{BC}{AC}=\frac{\sqrt{2}}{2}$,即$\frac{BC}{2+2\sqrt{2}}=\frac{\sqrt{2}}{2}$
∴BC=2+$\sqrt{2}$.
故选:A.
点评 本题主要考查的是动点问题的函数图象以及特殊锐角三角函数值,根据函数图象求得AD、DE的长度是解题的关键.

练习册系列答案
相关题目
17.实数π,$\frac{1}{5}$,$\sqrt{4}$,-1中,无理数是( )
| A. | π | B. | $\frac{1}{5}$ | C. | $\sqrt{4}$ | D. | -1 |
18. 近年来,“在初中数学教学中使用计算器是否直接影响学生计算能力的发展”这一问题受到了广泛关注,为此,某校随机调查了若干名学生对此问题的看法(看法分为三种:没有影响,影响不大,影响很大),并将调查结果绘制成如下不完整的统计表和统计图:
近年来,“在初中数学教学中使用计算器是否直接影响学生计算能力的发展”这一问题受到了广泛关注,为此,某校随机调查了若干名学生对此问题的看法(看法分为三种:没有影响,影响不大,影响很大),并将调查结果绘制成如下不完整的统计表和统计图:
学生对使用计算器影响计算能力发展的看法统计表
根据以上图表信息,解答下列问题:
(1)统计表中的m=40;
(2)统计图中表示“影响不大”的扇形的圆心角度数为108度;
(3)从这次接受调查的学生中随机调查一人,恰好是持“影响很大”看法的概率是多少?
 近年来,“在初中数学教学中使用计算器是否直接影响学生计算能力的发展”这一问题受到了广泛关注,为此,某校随机调查了若干名学生对此问题的看法(看法分为三种:没有影响,影响不大,影响很大),并将调查结果绘制成如下不完整的统计表和统计图:
近年来,“在初中数学教学中使用计算器是否直接影响学生计算能力的发展”这一问题受到了广泛关注,为此,某校随机调查了若干名学生对此问题的看法(看法分为三种:没有影响,影响不大,影响很大),并将调查结果绘制成如下不完整的统计表和统计图:学生对使用计算器影响计算能力发展的看法统计表
| 看法 | 没有影响 | 影响不大 | 影响很大 |
| 学生人数 | 100 | 60 | m |
(1)统计表中的m=40;
(2)统计图中表示“影响不大”的扇形的圆心角度数为108度;
(3)从这次接受调查的学生中随机调查一人,恰好是持“影响很大”看法的概率是多少?
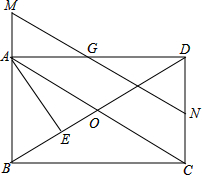 矩形ABCD中,N、G分别为CD、AD的中点,连接AC、BD交于O,连接NG并延长交BA的延长线于点M,NG交BD于点F,AE⊥BD于点E,则下列结论中:①MG=NG;②S△GDF:S△BOC=1:4;③BC2=2DE•OB;④图中有四对相似三角形,其中正确的结论有( )
矩形ABCD中,N、G分别为CD、AD的中点,连接AC、BD交于O,连接NG并延长交BA的延长线于点M,NG交BD于点F,AE⊥BD于点E,则下列结论中:①MG=NG;②S△GDF:S△BOC=1:4;③BC2=2DE•OB;④图中有四对相似三角形,其中正确的结论有( )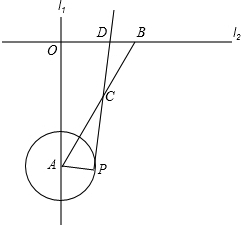 如图,直线l1⊥l2,垂足为O,点A、B分别在直线l1和l2上,∠OAB=30°,OB=2,以A为圆心,1为半径画圆,点P在圆A的圆周上运动,连接AP,过点P画PA的垂线与线段AB相交于点C,与直线l2相交于D,当AC=BC时,OD的长是1或4.
如图,直线l1⊥l2,垂足为O,点A、B分别在直线l1和l2上,∠OAB=30°,OB=2,以A为圆心,1为半径画圆,点P在圆A的圆周上运动,连接AP,过点P画PA的垂线与线段AB相交于点C,与直线l2相交于D,当AC=BC时,OD的长是1或4.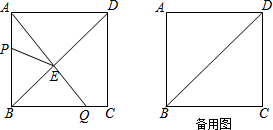
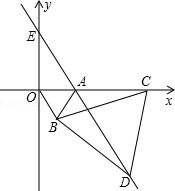 如图,直角坐标系中,点A的坐标为(1,0),以线段OA为边在第四象限内作等边△AOB,点C为x正半轴上一动点(OC>1),连接BC,以线段BC为边在第四象限内作等边△CBD,直线DA交y轴于点E.
如图,直角坐标系中,点A的坐标为(1,0),以线段OA为边在第四象限内作等边△AOB,点C为x正半轴上一动点(OC>1),连接BC,以线段BC为边在第四象限内作等边△CBD,直线DA交y轴于点E.