题目内容
6.已知|a-1|+|ab-2|=0,求$\frac{1}{ab}$+$\frac{1}{(a+1)(b+1)}$+$\frac{1}{(a+2)(b+2)}$+…+$\frac{1}{(a+98)(b+98)}$.分析 先根据非负数的性质求出ab的值,再代入原式进行计算即可.
解答 解:∵|a-1|+|ab-2|=0,
∴a-1=0,ab-2=0,解得a=1,b=2,
∴原式=$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{99×100}$
=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{99}$-$\frac{1}{100}$
=1-$\frac{1}{100}$
=$\frac{99}{100}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
16.某人购进一批苹果,到市场零售,已知卖出苹果数量x与售价y的关系如下表,写出用x表示y的关系式y=8.1x.
| 数量x(千克) | 2 | 3 | 4 | 5 |
| 售价y(元) | 16.2 | 24.3 | 32.4 | 40.5 |
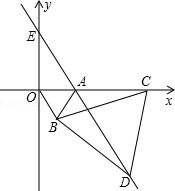 如图,直角坐标系中,点A的坐标为(1,0),以线段OA为边在第四象限内作等边△AOB,点C为x正半轴上一动点(OC>1),连接BC,以线段BC为边在第四象限内作等边△CBD,直线DA交y轴于点E.
如图,直角坐标系中,点A的坐标为(1,0),以线段OA为边在第四象限内作等边△AOB,点C为x正半轴上一动点(OC>1),连接BC,以线段BC为边在第四象限内作等边△CBD,直线DA交y轴于点E.
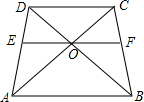 在梯形ABCD中,CD∥AB,AC、BD交于点O,过点O作AB的平行线交AD于点E,交BC于点F,则图中有5对相似形三角形;若DC=9,AB=15,则OD:OB=$\frac{3}{5}$,EF=$\frac{45}{4}$.
在梯形ABCD中,CD∥AB,AC、BD交于点O,过点O作AB的平行线交AD于点E,交BC于点F,则图中有5对相似形三角形;若DC=9,AB=15,则OD:OB=$\frac{3}{5}$,EF=$\frac{45}{4}$. 如图,AB∥CD,E是AD的中点,CF⊥AB,垂足为点F,求证:CE=EF.
如图,AB∥CD,E是AD的中点,CF⊥AB,垂足为点F,求证:CE=EF.