题目内容
4.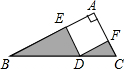 如图,Rt△ABC中,∠A=90°,四边形AEDF为正方形,E、D、F分别在Rt△ABC的三边上,BD=3,CD=2,则图中阴影部分的面积之和为3.
如图,Rt△ABC中,∠A=90°,四边形AEDF为正方形,E、D、F分别在Rt△ABC的三边上,BD=3,CD=2,则图中阴影部分的面积之和为3.
分析 首先过D点作DG⊥BC交AB于G.易证得△EDG≌△FDC,即可得DG=CD=4,则可得图中阴影部分的面积之和为S△BDE+S△DFC=S△BDE+S△EDG=S△BDG,继而求得答案.
解答  解:过D点作DG⊥BC交AB于G.
解:过D点作DG⊥BC交AB于G.
∴∠GDF+∠FDC=90°,
∵四边形AEDF为正方形,
∴DE=DF,∠EDF=∠AED=∠AFD=90°,
∴∠EDG+∠GDF=90°,
∴∠EDG=∠FDC,
在△EDG和△FDC中,
$\left\{\begin{array}{l}{∠GED=∠CFD=90°}\\{DE=DF}\\{∠EDG=∠FDC}\end{array}\right.$,
∴△EDG≌△FDC(ASA).
∴DG=CD=2.
∴阴影部分面积的和为:S△BDE+S△DFC=S△BDE+S△EDG=S△BDG=$\frac{1}{2}$BD•DG=$\frac{1}{2}$×3×2=3.
故答案为:3.
点评 此题考查了全等三角形的判定与性质、正方形的性质以及三角形的面积问题.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想与转化思想的应用.

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 如图,直线a∥b,被直线c所截,已知∠1=70°,那么∠2的度数为110°.
如图,直线a∥b,被直线c所截,已知∠1=70°,那么∠2的度数为110°.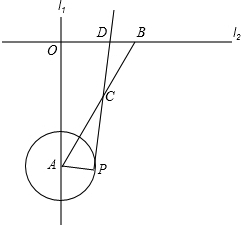 如图,直线l1⊥l2,垂足为O,点A、B分别在直线l1和l2上,∠OAB=30°,OB=2,以A为圆心,1为半径画圆,点P在圆A的圆周上运动,连接AP,过点P画PA的垂线与线段AB相交于点C,与直线l2相交于D,当AC=BC时,OD的长是1或4.
如图,直线l1⊥l2,垂足为O,点A、B分别在直线l1和l2上,∠OAB=30°,OB=2,以A为圆心,1为半径画圆,点P在圆A的圆周上运动,连接AP,过点P画PA的垂线与线段AB相交于点C,与直线l2相交于D,当AC=BC时,OD的长是1或4.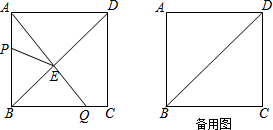
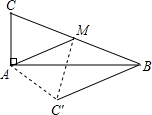 如图,在Rt△ABC中,∠BAC=90°,点M为斜边BC的中点,AM=5厘米,∠AMC=45°,将△AMC沿AM翻折,点C落在△ABC所在平面内的C′处,那么四边形BC′AC的面积为$\frac{25\sqrt{2}+25}{2}$平方厘米.
如图,在Rt△ABC中,∠BAC=90°,点M为斜边BC的中点,AM=5厘米,∠AMC=45°,将△AMC沿AM翻折,点C落在△ABC所在平面内的C′处,那么四边形BC′AC的面积为$\frac{25\sqrt{2}+25}{2}$平方厘米.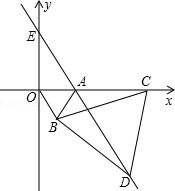 如图,直角坐标系中,点A的坐标为(1,0),以线段OA为边在第四象限内作等边△AOB,点C为x正半轴上一动点(OC>1),连接BC,以线段BC为边在第四象限内作等边△CBD,直线DA交y轴于点E.
如图,直角坐标系中,点A的坐标为(1,0),以线段OA为边在第四象限内作等边△AOB,点C为x正半轴上一动点(OC>1),连接BC,以线段BC为边在第四象限内作等边△CBD,直线DA交y轴于点E.