题目内容
11.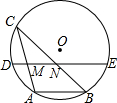 如图,⊙O的弦AB=4cm,点C为优弧$\widehat{AB}$上的动点,且∠ACB=30°.若弦DE经过弦AC、BC的中点M、N,则DM+EN的最大值是6cm.
如图,⊙O的弦AB=4cm,点C为优弧$\widehat{AB}$上的动点,且∠ACB=30°.若弦DE经过弦AC、BC的中点M、N,则DM+EN的最大值是6cm.
分析 由点M、N分别是AC、BC的中点,根据三角形中位线定理得出MN=$\frac{1}{2}$AB为定值,则NE+DM=DE-MN,所以当MN取最大值时,DM+EN有最大值.而直径是圆中最长的弦,故当DE为⊙O的直径时,可求得DM+EN的最大值.
解答 解:当DE为⊙O的直径时,DM+EN有最大值.
当DE为直径时,M点与O点重合,
∴AC也是直径,AC=8cm.
∵∠ABC是直径所对的圆周角,
∴∠ABC=90°,
∵∠C=30°,AB=4cm,
∴AB=$\frac{1}{2}$AC=8.
∵点M、N分别为AC、BC的中点,
∴MN=$\frac{1}{2}$AB=2,
∴DM+EN=DE-MN=8-2=6,
故答案为:6.
点评 本题考查的是三角形中位线定理、等边三角形的判定和性质和圆周角定理,综合运用以上定理是解题的关键,解答时,注意直径是圆中最长的弦.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
1.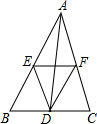 如图,点D、E、F分别为△ABC各边中点,下列说法正确的是( )
如图,点D、E、F分别为△ABC各边中点,下列说法正确的是( )
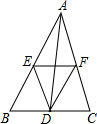 如图,点D、E、F分别为△ABC各边中点,下列说法正确的是( )
如图,点D、E、F分别为△ABC各边中点,下列说法正确的是( )| A. | DE=DF | B. | EF=$\frac{1}{2}$AB | C. | S△ABD=S△ACD | D. | AD平分∠BAC |
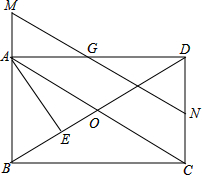 矩形ABCD中,N、G分别为CD、AD的中点,连接AC、BD交于O,连接NG并延长交BA的延长线于点M,NG交BD于点F,AE⊥BD于点E,则下列结论中:①MG=NG;②S△GDF:S△BOC=1:4;③BC2=2DE•OB;④图中有四对相似三角形,其中正确的结论有( )
矩形ABCD中,N、G分别为CD、AD的中点,连接AC、BD交于O,连接NG并延长交BA的延长线于点M,NG交BD于点F,AE⊥BD于点E,则下列结论中:①MG=NG;②S△GDF:S△BOC=1:4;③BC2=2DE•OB;④图中有四对相似三角形,其中正确的结论有( )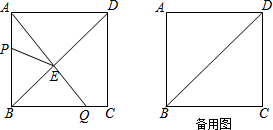
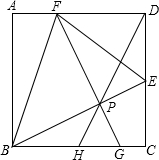 如图,点E,F分别在正方形ABCD的边CD、AD上,且AB=2CE=3AF,过点F作FG⊥BE于点P,交BC于点G,连接DP并延长交BC于点H,连接BF.EF.下列结论:
如图,点E,F分别在正方形ABCD的边CD、AD上,且AB=2CE=3AF,过点F作FG⊥BE于点P,交BC于点G,连接DP并延长交BC于点H,连接BF.EF.下列结论: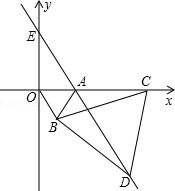 如图,直角坐标系中,点A的坐标为(1,0),以线段OA为边在第四象限内作等边△AOB,点C为x正半轴上一动点(OC>1),连接BC,以线段BC为边在第四象限内作等边△CBD,直线DA交y轴于点E.
如图,直角坐标系中,点A的坐标为(1,0),以线段OA为边在第四象限内作等边△AOB,点C为x正半轴上一动点(OC>1),连接BC,以线段BC为边在第四象限内作等边△CBD,直线DA交y轴于点E.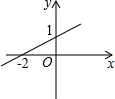 一次函数y=kx+b的图象如图所示,则由图象可知关于x的方程kx+b=0的解为x=-2.
一次函数y=kx+b的图象如图所示,则由图象可知关于x的方程kx+b=0的解为x=-2.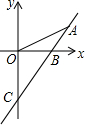 如图,直线y=kx-1与x轴、y轴分别交于B($\frac{1}{2}$,0),C(0,-1)两点.
如图,直线y=kx-1与x轴、y轴分别交于B($\frac{1}{2}$,0),C(0,-1)两点.