题目内容
8.(1)如图1,点P为△ABC的内角平分线BP与CP的交点,求证:∠BPC=90°+$\frac{1}{2}$∠A;(2)如图2,点P为△ABC内角平分线BP与外角平分线CP的交点,请直接写出∠BPC与∠A的关系;
(3)如图3,点P是△ABC的外角平分线BP与CP的交点,请直接∠BPC与∠A的关系.
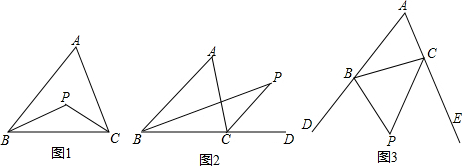
分析 (1)先根据三角形内角和定理求出∠PBC+∠PCB的度数,再根据角平分线的性质求出∠ABC+∠ACB的度数,由三角形内角和定理即可求出答案.
(2)根据角平分线的定义得∠PBC=$\frac{1}{2}$∠ABC,∠PCD=$\frac{1}{2}$∠ACD,再根据三角形外角性质得∠ACD=∠A+∠ABC,∠PCD=∠PBC+∠P,所以$\frac{1}{2}$(∠A+∠ABC)=∠PBC+∠P=$\frac{1}{2}$∠ABC+∠P,然后整理可得∠P=$\frac{1}{2}$∠A;
(3)根据题意得∠PBC=$\frac{1}{2}$(∠A+∠ACB),∠PCB=$\frac{1}{2}$(∠A+∠ABC),由三角形的内角和定理以及三角形外角的性质,求得∠P与∠A的关系,从而计算出∠P的度数.
解答 证明:(1)∵∠PBC+∠BCP+∠BPC=180°,
∵∠BPC=120°,
∴∠ABC+∠ACB=60°,
∵BP、CP是角平分线,
∴∠ABC=2∠PBC,∠ACB=2∠BCP,
∵∠ABC+∠ACB+∠A=180°,
∴∠BPC=90°+$\frac{1}{2}$∠A;
(2)∠P=$\frac{1}{2}$∠A,理由如下:
∵△ABC的内角平分线BP与外角平分线CP交于P,
∴∠PBC=$\frac{1}{2}$∠ABC,∠PCD=$\frac{1}{2}$∠ACD,
∵∠ACD=∠A+∠ABC,∠PCD=∠PBC+∠P,
∴$\frac{1}{2}$(∠A+∠ABC)=∠PBC+∠P=$\frac{1}{2}$∠ABC+∠P,
∴∠P=$\frac{1}{2}$∠A;
(3)∠P=90°-$\frac{1}{2}$∠A,理由如下:
∵BP、CP是△ABC的外角平分线,
∴∠PBC=$\frac{1}{2}$(∠A+∠ACB),∠PCB=$\frac{1}{2}$(∠A+∠ABC),
又∵∠PBC+∠PCB+∠P=180°,
∴∠P=180°-(∠PBC+∠PCB)
=180°-$\frac{1}{2}$(∠A+∠ACB+∠A+∠ABC)
=180°-$\frac{1}{2}$(180+∠A)
=90°-$\frac{1}{2}$∠A.
点评 本题考查的是三角形内角和定理及角平分线的性质,关键是根据由三角形的内角和定理以及三角形外角的性质,求得∠P与∠A的关系.

 53随堂测系列答案
53随堂测系列答案 近年来,“在初中数学教学中使用计算器是否直接影响学生计算能力的发展”这一问题受到了广泛关注,为此,某校随机调查了若干名学生对此问题的看法(看法分为三种:没有影响,影响不大,影响很大),并将调查结果绘制成如下不完整的统计表和统计图:
近年来,“在初中数学教学中使用计算器是否直接影响学生计算能力的发展”这一问题受到了广泛关注,为此,某校随机调查了若干名学生对此问题的看法(看法分为三种:没有影响,影响不大,影响很大),并将调查结果绘制成如下不完整的统计表和统计图:学生对使用计算器影响计算能力发展的看法统计表
| 看法 | 没有影响 | 影响不大 | 影响很大 |
| 学生人数 | 100 | 60 | m |
(1)统计表中的m=40;
(2)统计图中表示“影响不大”的扇形的圆心角度数为108度;
(3)从这次接受调查的学生中随机调查一人,恰好是持“影响很大”看法的概率是多少?
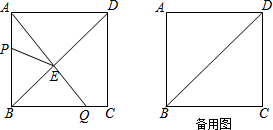
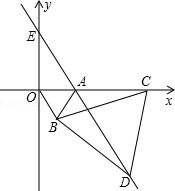 如图,直角坐标系中,点A的坐标为(1,0),以线段OA为边在第四象限内作等边△AOB,点C为x正半轴上一动点(OC>1),连接BC,以线段BC为边在第四象限内作等边△CBD,直线DA交y轴于点E.
如图,直角坐标系中,点A的坐标为(1,0),以线段OA为边在第四象限内作等边△AOB,点C为x正半轴上一动点(OC>1),连接BC,以线段BC为边在第四象限内作等边△CBD,直线DA交y轴于点E.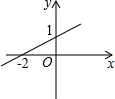 一次函数y=kx+b的图象如图所示,则由图象可知关于x的方程kx+b=0的解为x=-2.
一次函数y=kx+b的图象如图所示,则由图象可知关于x的方程kx+b=0的解为x=-2.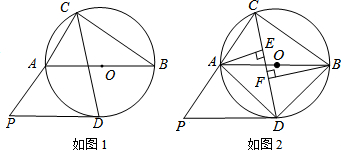
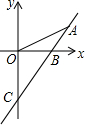 如图,直线y=kx-1与x轴、y轴分别交于B($\frac{1}{2}$,0),C(0,-1)两点.
如图,直线y=kx-1与x轴、y轴分别交于B($\frac{1}{2}$,0),C(0,-1)两点.
 如图,AB∥CD,E是AD的中点,CF⊥AB,垂足为点F,求证:CE=EF.
如图,AB∥CD,E是AD的中点,CF⊥AB,垂足为点F,求证:CE=EF.