题目内容
6.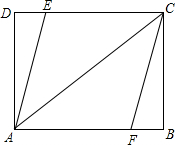 如图,矩形ABCD中,AB=8,AD=6,点E、F分别在边CD、AB上.
如图,矩形ABCD中,AB=8,AD=6,点E、F分别在边CD、AB上.(1)若DE=BF,求证:四边形AFCE是平行四边形;
(2)若四边形AFCE是菱形,求菱形AFCE的周长.
分析 (1)首先根据矩形的性质可得AB平行且等于CD,然后根据DE=BF,可得AF平行且等于CE,即可证明四边形AFCE是平行四边形;
(2)根据四边形AFCE是菱形,可得AE=CE,然后设DE=x,表示出AE,CE的长度,根据相等求出x的值,继而可求得菱形的边长及周长.
解答 解;(1)∵四边形ABCD为矩形,
∴AB=CD,AB∥CD,
∵DE=BF,
∴AF=CE,AF∥CE,
∴四边形AFCE是平行四边形;
(2)∵四边形AFCE是菱形,
∴AE=CE,
设DE=x,
则AE=$\sqrt{{6}^{2}+{x}^{2}}$,CE=8-x,
则$\sqrt{{6}^{2}+{x}^{2}}$=8-x,
化简有16x-28=0,
解得:x=$\frac{7}{4}$,
将x=$\frac{7}{4}$代入原方程检验可得等式两边相等,
即x=$\frac{7}{4}$为方程的解.
则菱形的边长为:8-$\frac{7}{4}$=$\frac{25}{4}$,
周长为:4×$\frac{25}{4}$=25,
故菱形AFCE的周长为25.
点评 本题考查了矩形的性质和菱形的性质,解答本题的关键是则矩形对边平行且相等的性质以及菱形四条边相等的性质.

练习册系列答案
相关题目
17.实数π,$\frac{1}{5}$,$\sqrt{4}$,-1中,无理数是( )
| A. | π | B. | $\frac{1}{5}$ | C. | $\sqrt{4}$ | D. | -1 |
1.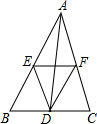 如图,点D、E、F分别为△ABC各边中点,下列说法正确的是( )
如图,点D、E、F分别为△ABC各边中点,下列说法正确的是( )
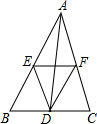 如图,点D、E、F分别为△ABC各边中点,下列说法正确的是( )
如图,点D、E、F分别为△ABC各边中点,下列说法正确的是( )| A. | DE=DF | B. | EF=$\frac{1}{2}$AB | C. | S△ABD=S△ACD | D. | AD平分∠BAC |
18. 近年来,“在初中数学教学中使用计算器是否直接影响学生计算能力的发展”这一问题受到了广泛关注,为此,某校随机调查了若干名学生对此问题的看法(看法分为三种:没有影响,影响不大,影响很大),并将调查结果绘制成如下不完整的统计表和统计图:
近年来,“在初中数学教学中使用计算器是否直接影响学生计算能力的发展”这一问题受到了广泛关注,为此,某校随机调查了若干名学生对此问题的看法(看法分为三种:没有影响,影响不大,影响很大),并将调查结果绘制成如下不完整的统计表和统计图:
学生对使用计算器影响计算能力发展的看法统计表
根据以上图表信息,解答下列问题:
(1)统计表中的m=40;
(2)统计图中表示“影响不大”的扇形的圆心角度数为108度;
(3)从这次接受调查的学生中随机调查一人,恰好是持“影响很大”看法的概率是多少?
 近年来,“在初中数学教学中使用计算器是否直接影响学生计算能力的发展”这一问题受到了广泛关注,为此,某校随机调查了若干名学生对此问题的看法(看法分为三种:没有影响,影响不大,影响很大),并将调查结果绘制成如下不完整的统计表和统计图:
近年来,“在初中数学教学中使用计算器是否直接影响学生计算能力的发展”这一问题受到了广泛关注,为此,某校随机调查了若干名学生对此问题的看法(看法分为三种:没有影响,影响不大,影响很大),并将调查结果绘制成如下不完整的统计表和统计图:学生对使用计算器影响计算能力发展的看法统计表
| 看法 | 没有影响 | 影响不大 | 影响很大 |
| 学生人数 | 100 | 60 | m |
(1)统计表中的m=40;
(2)统计图中表示“影响不大”的扇形的圆心角度数为108度;
(3)从这次接受调查的学生中随机调查一人,恰好是持“影响很大”看法的概率是多少?
 如图,直线a∥b,被直线c所截,已知∠1=70°,那么∠2的度数为110°.
如图,直线a∥b,被直线c所截,已知∠1=70°,那么∠2的度数为110°.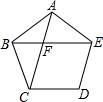 如图,在正五边形ABCDE中,对角线AC、BE相交于点F,则F为线段BE的黄金分割点,若EF=2,则BE=$\sqrt{5}$+1.
如图,在正五边形ABCDE中,对角线AC、BE相交于点F,则F为线段BE的黄金分割点,若EF=2,则BE=$\sqrt{5}$+1.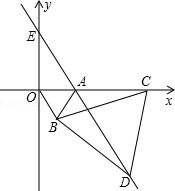 如图,直角坐标系中,点A的坐标为(1,0),以线段OA为边在第四象限内作等边△AOB,点C为x正半轴上一动点(OC>1),连接BC,以线段BC为边在第四象限内作等边△CBD,直线DA交y轴于点E.
如图,直角坐标系中,点A的坐标为(1,0),以线段OA为边在第四象限内作等边△AOB,点C为x正半轴上一动点(OC>1),连接BC,以线段BC为边在第四象限内作等边△CBD,直线DA交y轴于点E.