题目内容
 如图所示,已知在Rt△ABC中,CD是斜边AB上的高,若AD=8cm,BD=2cm,求CD的长.
如图所示,已知在Rt△ABC中,CD是斜边AB上的高,若AD=8cm,BD=2cm,求CD的长.考点:相似三角形的判定与性质,射影定理
专题:
分析:由条件可以证明出△ADC∽△CDB,从而就有
=
,再将AD、BD的值代入比例式就可以求出结论.
| AD |
| CD |
| CD |
| BD |
解答: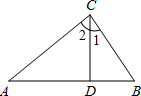 解:如图,
解:如图,
∵CD⊥AB,
∴∠ADC=∠BDC=90°.
∴∠2+∠A=90°,∠1+∠B=90°.
∵△ABC是Rt△,
∴∠1+∠2=90°,
∴∠A=∠1,∠B=∠2,
∴△ADC∽△CDB,
∴
=
,.
∵AD=8cm,BD=2cm,
∴
=
,
∴CD=4cm.
 解:如图,
解:如图,∵CD⊥AB,
∴∠ADC=∠BDC=90°.
∴∠2+∠A=90°,∠1+∠B=90°.
∵△ABC是Rt△,
∴∠1+∠2=90°,
∴∠A=∠1,∠B=∠2,
∴△ADC∽△CDB,
∴
| AD |
| CD |
| CD |
| BD |
∵AD=8cm,BD=2cm,
∴
| 8 |
| CD |
| CD |
| 2 |
∴CD=4cm.
点评:本题考查了直角三角形的性质和相似三角形的判定及性质的运用,在解答时运用直角三角形的性质求出角相等证明三角形相似是关健.

练习册系列答案
相关题目
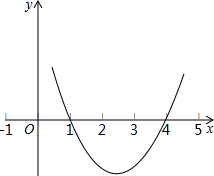 已知二次函数y=ax2-5x+c的图象如图所示.
已知二次函数y=ax2-5x+c的图象如图所示.