题目内容
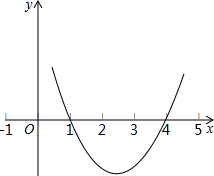 已知二次函数y=ax2-5x+c的图象如图所示.
已知二次函数y=ax2-5x+c的图象如图所示.(1)求a、c的值;
(2)当x取什么值时,函数值y随x的增大而增大?
考点:抛物线与x轴的交点
专题:
分析:(1)由图象可知:抛物线与x轴的交点为(1,0),(4,0),a>0;代入解析式即可求得;
(2)根据二次函数的解析式求得对称轴x=
,即可判定函数值y随x的增大而增大时x的取值.
(2)根据二次函数的解析式求得对称轴x=
| 5 |
| 2 |
解答:解:(1)由图象可知:抛物线与x轴的交点为(1,0),(4,0),a>0;
则
,
解得
;
(2)∵
,
∴抛物线的解析式为y=x2-5x+4,
∵对称轴x=-
=-
=
,
∴当x>
时,函数值y随x的增大而增大;
则
|
解得
|
(2)∵
|
∴抛物线的解析式为y=x2-5x+4,
∵对称轴x=-
| b |
| 2a |
| -5 |
| 2 |
| 5 |
| 2 |
∴当x>
| 5 |
| 2 |
点评:本题考查了待定系数法求解析式和抛物线的对称轴,以及抛物线的性质等,题型较简单,熟练掌握抛物线的性质是关键.

练习册系列答案
相关题目
 如图,锐角△ABC中,BD是∠ABC的角平分线,M、N分别是BD、BC线段上运动的点,S△ABC=8,AB=4,求:MN+MC的最小值是多少?
如图,锐角△ABC中,BD是∠ABC的角平分线,M、N分别是BD、BC线段上运动的点,S△ABC=8,AB=4,求:MN+MC的最小值是多少?
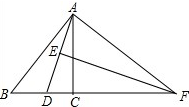 如图,已知△ABC中,AD平分∠BAC,EF是AD的垂直平分线,交BC延长线于F,求证:DF2=BF•CF.
如图,已知△ABC中,AD平分∠BAC,EF是AD的垂直平分线,交BC延长线于F,求证:DF2=BF•CF.
 如图所示,已知在Rt△ABC中,CD是斜边AB上的高,若AD=8cm,BD=2cm,求CD的长.
如图所示,已知在Rt△ABC中,CD是斜边AB上的高,若AD=8cm,BD=2cm,求CD的长.