题目内容
解方程:x2+x+2x
=14.
| x+2 |
考点:无理方程
专题:解题思想
分析:先将原方程配方,然后再开方得两个无理方程:x+
=4①,x+
=-4②,然后再利用换元的思想,将方程①、②化为有理方程,y2+y-6=0③和w2+w+2=0④,进一步解方程③、④,最后将y、w的值代入从而确定原方程的解.
| x+2 |
| x+2 |
解答:解:x2+x+2x
=14
配方得:x2+2x•
+(x+2)=16
即:(x+
)2=16
开方得:x+
=±4
∴x+
=4①或x+
=-4②
解①:方程①可化为x+2+
=6
设
=y,则x+2=y2.
∴原方程可化为y2+y-6=0
解得:y1=2,y2=-3
当y1=2时,
=2
两边同时平方得:x+2=4
解得:x1=2
当y2=-3时,
=-3(无意义)
∴此方程无解.
解②:方程②可化为x+2+
=-2
设
=w,则x+2=w2
∴原方程可化为w2+w+2=0
∵△=-7<0
∴此方程无解.
总上所述原方程的解为x=2.
| x+2 |
配方得:x2+2x•
| x+2 |
即:(x+
| x+2 |
开方得:x+
| x+2 |
∴x+
| x+2 |
| x+2 |
解①:方程①可化为x+2+
| x+2 |
设
| x+2 |
∴原方程可化为y2+y-6=0
解得:y1=2,y2=-3
当y1=2时,
| x+2 |
两边同时平方得:x+2=4
解得:x1=2
当y2=-3时,
| x+2 |
∴此方程无解.
解②:方程②可化为x+2+
| x+2 |
设
| x+2 |
∴原方程可化为w2+w+2=0
∵△=-7<0
∴此方程无解.
总上所述原方程的解为x=2.
点评:本题主要考查了无理方程的求解方法,其基本解题思想是化无理方程为有理方程,进而确定原方程的解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,已知在△ABC中,AB=AC,点E在CA的延长线上,ED⊥BC于D.求证:AE=AF.
如图,已知在△ABC中,AB=AC,点E在CA的延长线上,ED⊥BC于D.求证:AE=AF.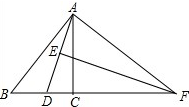 如图,已知△ABC中,AD平分∠BAC,EF是AD的垂直平分线,交BC延长线于F,求证:DF2=BF•CF.
如图,已知△ABC中,AD平分∠BAC,EF是AD的垂直平分线,交BC延长线于F,求证:DF2=BF•CF. 如图所示,已知在Rt△ABC中,CD是斜边AB上的高,若AD=8cm,BD=2cm,求CD的长.
如图所示,已知在Rt△ABC中,CD是斜边AB上的高,若AD=8cm,BD=2cm,求CD的长.