题目内容
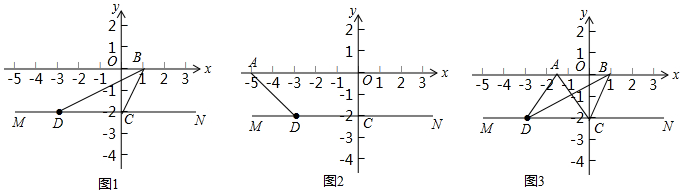
9.在平面直角坐标系中,A为x轴负半轴上一点.B为x轴上一点,C(0,-2),D(-3,-2),直线MN经过C、D两点.(1)如图1.求△BCD的面积.
(2)如图2,若A(-5,0),当BC=AD时,请尺规作图在图2中作出点B的位置,并直接写出点B的坐标.
(3)如图3,当B恰好为∠ADC和∠ACN的角平分线交点时,记∠BDC=α,∠BCN=β,求∠DBC和∠DAC的度数(用含α、β的式子表示).并写出∠DAC和∠DBC之间的数量关系.
分析 (1)先确定出OC,CD,在用三角形的面积公式即可得出结论;
(2)以点C为圆心,AD长为半径画弧和x轴的交点即为所求的点,然后根据两点间的距离公式建立方程即可求出点B的坐标;
(3)先根据角平分线的定义得出,∠ADC=2α,∠ACN=2β,再用三角形的外角的性质即可得出结论.
解答 解:(1)C(0,-2),D(-3,-2),
∴OC=2,CD=0+3=3,
∵点B在x轴上,
∴S△BCD=$\frac{1}{2}$CD•OC=$\frac{1}{2}$×3×2=3;
(2)如图2,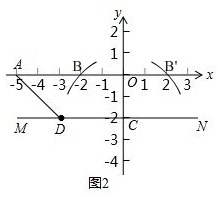
以点C为为圆心,AD长为半径画弧与x交于点B和B',
∴满足条件的点B如图2所示的点B和B'的位置,
∵A(-5,0),D(-3,-2),
∴AD=$\sqrt{4+4}$=2$\sqrt{2}$,
设B(m,0),
∵C(0,-2),
∴BC=$\sqrt{{m}^{2}+4}$,
∴m=±2,
∴B(-2,0)或(2,0);
(3)∵BD是∠ADC的平分线,
∴∠ADC=2∠BDC=2α,
∵BC是∠BCN的角平分线,
∴∠ACN=2∠BCN=2β,
∵∠ACD是△ACD的外角,
∴∠ACN=∠ADC+∠CAD,
∴∠CAD=∠ACN-∠ADC=2α-2β=2(α-β),
∵∠BCN是△BCD的外角,
∴∠BCN=∠BDC+∠DBC,
∴∠DBC=∠BCN-∠BDC=α-β,
∴∠DAC=2∠DBC.
点评 此题是三角形综合题,主要考查了三角形的面积公式,两点间的距离公式,基本作图,三角形的外角的性质,角平分线的定义,解(1)的关键是求出OC,CD,解(2)的关键是作出图形,解(3)的关键是利用三角形的外角的性质得出∠CAD=2(α-β),∠DB=α-β,是一道基础题目.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
19.下列性质中,直角三角形具有而等腰三角形不一定具有的是( )
| A. | 两边之和大于第三边 | |
| B. | 内角和等于180° | |
| C. | 有两个锐角的和等于90° | |
| D. | 有一个角的平分线垂直于这个角的对边 |
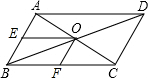 如图,在平行四边形ABCD中,BD为对角线,点E、O、F分别是AB、BD、BC的中点,且OE=3,OF=2,则平行四边形ABCD的周长为20.
如图,在平行四边形ABCD中,BD为对角线,点E、O、F分别是AB、BD、BC的中点,且OE=3,OF=2,则平行四边形ABCD的周长为20. 如图,已知平行四边形ABCD中,△DEC和△FBC是等边三角形,则∠AEF=60°.
如图,已知平行四边形ABCD中,△DEC和△FBC是等边三角形,则∠AEF=60°.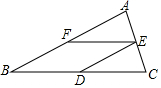 如图,在△ABC中,AB=BC,D、E、F分别是BC、AC、AB边上的中点.
如图,在△ABC中,AB=BC,D、E、F分别是BC、AC、AB边上的中点. 如图,AO⊥BC,DO⊥OE,则∠1+∠2=90°,∠3+∠2=90°,所以∠1=∠3,其依据是同角的余角相等.
如图,AO⊥BC,DO⊥OE,则∠1+∠2=90°,∠3+∠2=90°,所以∠1=∠3,其依据是同角的余角相等.