题目内容
1.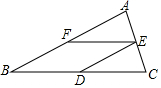 如图,在△ABC中,AB=BC,D、E、F分别是BC、AC、AB边上的中点.
如图,在△ABC中,AB=BC,D、E、F分别是BC、AC、AB边上的中点.(1)求证:四边形BDEF是菱形;
(2)若AB=12cm,求菱形BDEF的周长.
(3)如果S△AEF=1cm2,则S△ABC=4 cm2(直接写出答案)
分析 (1)可根据菱形的定义“一组邻边相等的平行四边形是菱形”,先证明四边形BFED是平行四边形,然后再证明四边形的邻边相等即可;
(2)F是AB的中点,有了AB的长也就求出了菱形的边长BF的长,那么菱形BDEF的周长也就能求出了;
(3)由EF∥BC,可知△AFE∽△ABC,即可推出$\frac{{S}_{△AFE}}{{S}_{△ABC}}$=($\frac{EF}{BC}$)2=$\frac{1}{4}$,由此即可解决问题;
解答 (1)证明:∵D、E、F分别是BC、AC、AB的中点,
∴DE∥AB,EF∥BC,
∴四边形BDEF是平行四边形,
又∵DE=$\frac{1}{2}$AB,EF=$\frac{1}{2}$BC,且AB=BC,
∴DE=EF,
∴四边形BDEF是菱形;
(2)解:∵AB=12cm,F为AB中点,
∴BF=6cm,
∴菱形BDEF的周长为6×4=24cm.
(3)∵EF∥BC,
∴△AFE∽△ABC,
∴$\frac{{S}_{△AFE}}{{S}_{△ABC}}$=($\frac{EF}{BC}$)2=$\frac{1}{4}$,
∵S△AFE=1,
∴S△ABC=4,
故答案为4.
点评 本题考查菱形的判定和性质、三角形的中位线定理,平行线的性质,相似三角形的判定和性质等知识,解题的关键是判断四边形BDEF是菱形,灵活运用所学知识解决问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.下列说法中,正确的是( )
| A. | 对角线相等的四边形是矩形 | |
| B. | 对角线互相平分的四边形是平行四边形 | |
| C. | 对角线平分一组对角的四边形是菱形 | |
| D. | 对角线互相垂直的四边形是菱形 |
11.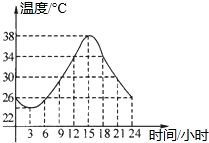 如图是某市一天的温度随时间变化的大致图象,则下列说法中错误的是( )
如图是某市一天的温度随时间变化的大致图象,则下列说法中错误的是( )
 如图是某市一天的温度随时间变化的大致图象,则下列说法中错误的是( )
如图是某市一天的温度随时间变化的大致图象,则下列说法中错误的是( )| A. | 这天15时的温度最高 | |
| B. | 这天3时的温度最低 | |
| C. | 这天21时的温度是30℃ | |
| D. | 这天最高温度与最低温度的差是13℃ |
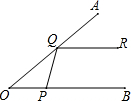 如图,已知∠AOB=40°,在∠AOB的两边OA、OB上分别存在点Q、点P,过点Q作直线QR∥OB,当OP=QP时,∠PQR的度数是100°.
如图,已知∠AOB=40°,在∠AOB的两边OA、OB上分别存在点Q、点P,过点Q作直线QR∥OB,当OP=QP时,∠PQR的度数是100°.