题目内容
4.计算:$\sqrt{\frac{9}{4}}$-$\root{3}{\frac{27}{64}}$+$\sqrt{(-\frac{1}{4})^{2}}$.分析 原式利用平方根、立方根定义计算即可得到结果.
解答 解:原式=$\frac{3}{2}$-$\frac{3}{4}$+$\frac{1}{4}$=1.
点评 此题考查了实数的运算,以及平方根、立方根,熟练掌握各自的性质是解本题的关键.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
19.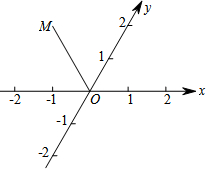 在平面上,过一定点O作两条斜交的轴x和y,它们的交角是ω(ω≠90°),以定点O为原点,在每条轴上取相同的单位长度,这样就在平面上建立了一个斜角坐标系,其中ω叫做坐标角.对于平面内任意一点P,过P作x轴和y轴的平行线,与两轴分别交于A和B,它们在两轴的坐标分别是x和y,于是点P的坐标就是(x,y).如图,ω=60°,且y轴平分∠MOx,OM=2,则点M的坐标是( )
在平面上,过一定点O作两条斜交的轴x和y,它们的交角是ω(ω≠90°),以定点O为原点,在每条轴上取相同的单位长度,这样就在平面上建立了一个斜角坐标系,其中ω叫做坐标角.对于平面内任意一点P,过P作x轴和y轴的平行线,与两轴分别交于A和B,它们在两轴的坐标分别是x和y,于是点P的坐标就是(x,y).如图,ω=60°,且y轴平分∠MOx,OM=2,则点M的坐标是( )
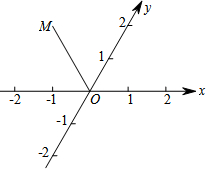 在平面上,过一定点O作两条斜交的轴x和y,它们的交角是ω(ω≠90°),以定点O为原点,在每条轴上取相同的单位长度,这样就在平面上建立了一个斜角坐标系,其中ω叫做坐标角.对于平面内任意一点P,过P作x轴和y轴的平行线,与两轴分别交于A和B,它们在两轴的坐标分别是x和y,于是点P的坐标就是(x,y).如图,ω=60°,且y轴平分∠MOx,OM=2,则点M的坐标是( )
在平面上,过一定点O作两条斜交的轴x和y,它们的交角是ω(ω≠90°),以定点O为原点,在每条轴上取相同的单位长度,这样就在平面上建立了一个斜角坐标系,其中ω叫做坐标角.对于平面内任意一点P,过P作x轴和y轴的平行线,与两轴分别交于A和B,它们在两轴的坐标分别是x和y,于是点P的坐标就是(x,y).如图,ω=60°,且y轴平分∠MOx,OM=2,则点M的坐标是( )| A. | (2,-2) | B. | (-1,2) | C. | (-2,2) | D. | (-2,1) |
16.下列说法中,正确的是( )
| A. | 对角线相等的四边形是矩形 | |
| B. | 对角线互相平分的四边形是平行四边形 | |
| C. | 对角线平分一组对角的四边形是菱形 | |
| D. | 对角线互相垂直的四边形是菱形 |
14.下列说法不正确的是( )
| A. | 全等三角形的对应边相等 | |
| B. | 两角一边对应相等的两个三角形全等 | |
| C. | 三边对应相等的两个三角形全等 | |
| D. | 两边一角分别相等的三角形全等 |
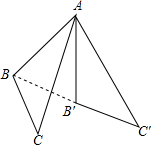 △ABC以点A为旋转中心,按逆时针方向旋转60°,得△AB′C′,则∠BAB′的度数是60°.
△ABC以点A为旋转中心,按逆时针方向旋转60°,得△AB′C′,则∠BAB′的度数是60°.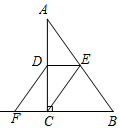 已知:如图,△ABC中,∠ACB=90°,点D、E分别是AC、AB的中点,点F在BC的延长线上,且∠CDF=∠A.求证:四边形DECF是平行四边形.
已知:如图,△ABC中,∠ACB=90°,点D、E分别是AC、AB的中点,点F在BC的延长线上,且∠CDF=∠A.求证:四边形DECF是平行四边形.