题目内容
16. 如图,在菱形ABCD中,∠A=100°,E,F分别是边AB和BC的中点,EP⊥CD于点P.
如图,在菱形ABCD中,∠A=100°,E,F分别是边AB和BC的中点,EP⊥CD于点P.①EF=PF,②∠EPF=40°,③ED-PC=EP,④S△PEF=$\frac{1}{2}$S四边形BEPC
其中正确的序号有①②④.
分析 ①②正确,延长EF交DC的延长线于H点.只要证明△BEF≌△CHF即可解决问题;
③错误.由图象可知,PC<BE,则可在线段DP上取一点Q,使得PQ=PC,在△EPQ中,EQ>EP+PQ,易知ED>EQ,推出DE>EP+PQ=EP+PC,推出ED-PC>EP;
④正确.首先证明S四边形BCPH=S△EPH,再证明S△PEF=$\frac{1}{2}$即可解决问题;
解答 解:延长EF交DC的延长线于H点.
∵在菱形ABCD中,∠A=100°,E,F分别是边AB和BC的中点,
∴∠B=80°,BE=BF.
∴∠BEF=(180°-80°)÷2=50°.
∵AB∥DC,∴∠FHC=∠BEF=50°,
又∵BF=FC,∠B=∠FCH,
∴△BEF≌△CHF.
∴EF=FH.
∵EP⊥DC,
∴∠EPH=90°.
∴FP=FH=EF,则∠FPC=∠FHP=∠BEF=50°,
∴∠EPF=40°,故①②正确,
∵由图象可知,PC<BE,则可在线段DP上取一点Q,使得PQ=PC,
在△EPQ中,EQ>EP+PQ,易知ED>EQ,
∴DE>EP+PQ=EP+PC,
∴ED-PC>EP,故③错误,
∵EF=FH,
∴S△EFP=S△PFH,
∴S△PEF=$\frac{1}{2}$S△EPH,
∵S△BEF=S△CFH,
∴S四边形BCPH=S△EPH,
∴S△PEF=$\frac{1}{2}$S四边形BCPE,故④正确.
故答案为①②④.
点评 此题考查了菱形的性质、全等三角形的判定方法、直角三角形斜边上的中线等于斜边的一半等知识点,综合性较强.如何作出辅助线是难点.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
8. 如图,在周长为10cm的?ABCD中,AB≠AD,AC、BD相交于点O,OE⊥BD于E,则△ABE的周长为( )
如图,在周长为10cm的?ABCD中,AB≠AD,AC、BD相交于点O,OE⊥BD于E,则△ABE的周长为( )
 如图,在周长为10cm的?ABCD中,AB≠AD,AC、BD相交于点O,OE⊥BD于E,则△ABE的周长为( )
如图,在周长为10cm的?ABCD中,AB≠AD,AC、BD相交于点O,OE⊥BD于E,则△ABE的周长为( )| A. | 5cm | B. | 4cm | C. | 3cm | D. | 2cm |
5. 如图,直线y1=$\frac{3}{2}$x与直线y2=-$\frac{1}{2}$x+2交于点A,若y1≤y2,则( )
如图,直线y1=$\frac{3}{2}$x与直线y2=-$\frac{1}{2}$x+2交于点A,若y1≤y2,则( )
 如图,直线y1=$\frac{3}{2}$x与直线y2=-$\frac{1}{2}$x+2交于点A,若y1≤y2,则( )
如图,直线y1=$\frac{3}{2}$x与直线y2=-$\frac{1}{2}$x+2交于点A,若y1≤y2,则( )| A. | x≥1 | B. | x≤1 | C. | x$≥\frac{3}{2}$ | D. | x$≤\frac{3}{2}$ |
 如图,在△ABC中,∠C=90°,CD⊥AB于D,AC=6,BC=8.求CD的长.
如图,在△ABC中,∠C=90°,CD⊥AB于D,AC=6,BC=8.求CD的长.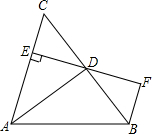 如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AB=2BF,其中正确的结论有①②③.
如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AB=2BF,其中正确的结论有①②③.