题目内容
6.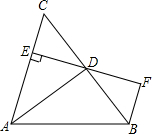 如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AB=2BF,其中正确的结论有①②③.
如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AB=2BF,其中正确的结论有①②③.
分析 首先证明AB=AC,根据等腰三角形的性质即可判断②③正确,由△CDE≌△DBF,推出DE=DF,CE=BF,故①正确;由AE=2BF,推出AC=3BF,故④错误;
解答 解:∵BF∥AC,
∴∠C=∠CBF,
∵BC平分∠ABF,
∴∠ABC=∠CBF,
∴∠C=∠ABC,
∴AB=AC,
∵AD是△ABC的角平分线,
∴BD=CD,AD⊥BC,故②③正确,
在△CDE与△DBF中,
$\left\{\begin{array}{l}{∠EDC=∠BDF}\\{CD=BD}\\{∠C=∠CBF}\end{array}\right.$,
∴△CDE≌△DBF,
∴DE=DF,CE=BF,故①正确;
∵AE=2BF,
∴AC=3BF,故④错误;
故答案为①②③.
点评 本题考查了全等三角形的判定和性质,等腰三角形的性质,平行线的性质等知识,解题的关键是正确使用等腰三角形的性质三线合一,属于中考常考题型.

练习册系列答案
相关题目
16.如果a>b,那么下列结论一定正确的是( )
| A. | a-5<b-5 | B. | 5-a<5-b | C. | ac2>bc2 | D. | a2>b2 |
 如图,在菱形ABCD中,∠A=100°,E,F分别是边AB和BC的中点,EP⊥CD于点P.
如图,在菱形ABCD中,∠A=100°,E,F分别是边AB和BC的中点,EP⊥CD于点P.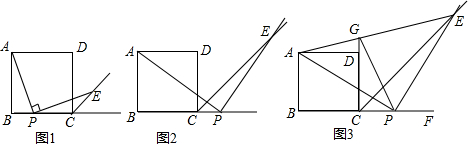
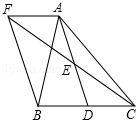 如图,点D是△ABC的边BC上一点,点E是AD的中点,过点A作AF∥BC,交CE的延长线于F,连接BF.
如图,点D是△ABC的边BC上一点,点E是AD的中点,过点A作AF∥BC,交CE的延长线于F,连接BF. 如图,将矩形ABCD绕点C顺时针旋转90°得到矩形FGCE,点M、N分别是BD、GE的中点,若BC=7,CE=1,则MN的长( )
如图,将矩形ABCD绕点C顺时针旋转90°得到矩形FGCE,点M、N分别是BD、GE的中点,若BC=7,CE=1,则MN的长( )