题目内容
15.解方程:|3x+1|-|1-x|=2.分析 分别讨论①x≥1②-$\frac{1}{3}$≤x<1③x<-$\frac{1}{3}$,根据x的范围去掉绝对值,解出x,综合三种情况可得出x的最终范围.
解答 解:①当x≥1时,3x+1+1-x=2,
x=0,不存在;
②当-$\frac{1}{3}$≤x<1时,3x+1+x-1=2,x=$\frac{1}{2}$;
③当x<-$\frac{1}{3}$时,-3x-1-1+x=2,x=-2,
∴|3x+1|-|1-x|=2的解是-$\frac{1}{3}$≤x<1时,x=$\frac{1}{2}$;x<-$\frac{1}{3}$时x=-2.
点评 本题考查了含绝对值符号的一元一次方程,分类讨论是解题关键,意最后的解可以联合起来,难度很大.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
10.甲乙两家商场平时以同样的价格出售相同的商品.春节期间两家商场都让利酬宾,其中甲商场所有商品按8折出售,乙商场对一次购物中超过200元后的价格部分打7折.
设x(单位:元)表示商品原价,y(单位:元)表示购物金额.
(Ⅰ)根据题意,填写下表:(单位:元)
(Ⅱ)分别就两家商场的让利方式,写出y关于x的函数解析式;
(Ⅲ)春节期间,当在同一商场累计购物超过200元时,哪家商场的实际花费少?
设x(单位:元)表示商品原价,y(单位:元)表示购物金额.
(Ⅰ)根据题意,填写下表:(单位:元)
| 商品价格 购物金额 | 120 | 180 | 200 | 260 |
| 甲商场 | 96 | 144 | 160 | 208 |
| 乙商场 | 120 | 200 | 200 | ,242 |
(Ⅲ)春节期间,当在同一商场累计购物超过200元时,哪家商场的实际花费少?
7.近几年,全社会对空气污染问题越来越重视,空气净化器的销量也在逐年增加.某商场从厂家购进了A、B两种型号的空气净化器,两种净化器的销售相关信息见下表:
(1)每台A型空气净化器和B型空气净化器的销售利润分别是多少?
(2)该公司计划一次购进两种型号的空气净化器共100台,其中B型空气净化器的进货量不少于A型空气净化器的2倍,为使该公司销售完这100台空气净化器后的总利润最大,请你设计相应的进货方案;
(3)已知A型空气净化器的净化能力为300m3/小时,B型空气净化器的净化能力为200m3/小时,某长方体室内活动场地的总面积为200m2,室内墙高3m,该场地负责人计划购买5台空气净化器每天花费30分钟将室内就欧诺个气净化一新,若不考虑空气对流等因素,至少要购买A型空气净化器多少台?
| A型销售数量(台) | B型销售数量(台) | 总利润(元) |
| 5 | 10 | 2000 |
| 10 | 5 | 2500 |
(2)该公司计划一次购进两种型号的空气净化器共100台,其中B型空气净化器的进货量不少于A型空气净化器的2倍,为使该公司销售完这100台空气净化器后的总利润最大,请你设计相应的进货方案;
(3)已知A型空气净化器的净化能力为300m3/小时,B型空气净化器的净化能力为200m3/小时,某长方体室内活动场地的总面积为200m2,室内墙高3m,该场地负责人计划购买5台空气净化器每天花费30分钟将室内就欧诺个气净化一新,若不考虑空气对流等因素,至少要购买A型空气净化器多少台?
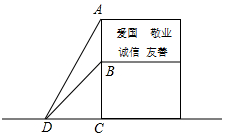 为了弘扬“社会主义核心价值观”,区政府在广场上竖立了如图所示的公益广告牌,并在两侧加固钢缆,已知钢缆底端D到达广告牌立柱AC的距离为5米,从点D测得广告牌顶端A点和底端B点的仰角分别为60°和45°,求广告牌的高度AB.
为了弘扬“社会主义核心价值观”,区政府在广场上竖立了如图所示的公益广告牌,并在两侧加固钢缆,已知钢缆底端D到达广告牌立柱AC的距离为5米,从点D测得广告牌顶端A点和底端B点的仰角分别为60°和45°,求广告牌的高度AB.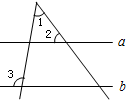 如图,直线a∥b,若∠1=55°,∠2=60°,则∠3=115°.
如图,直线a∥b,若∠1=55°,∠2=60°,则∠3=115°.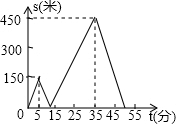 甲乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走.设甲乙两人相距s(米),甲行走的时间为t(分),s关于t的函数函数图象的一部分如图所示.当甲乙两人相距360米时,求所有符合条件的t的值的和为68.5.
甲乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走.设甲乙两人相距s(米),甲行走的时间为t(分),s关于t的函数函数图象的一部分如图所示.当甲乙两人相距360米时,求所有符合条件的t的值的和为68.5.