题目内容
5.为了响应市政府“创建文明城市,建设美丽莆田”的号召,某街道决定从备选的五种树中选购一种进行栽种.工作人员在街道辖区范围内随机抽取了部分居民,进行“我最喜欢的一种树”的调查活动(每人限选其中一种树),并将调查结果整理后,绘制成如图两个不完整的统计图:请根据所给信息解答以下问题:
(1)这次参与调查的居民人数为200人;
(2)扇形统计图中“枫树”所在扇形的圆心角度数为36°;
(3)已知该街道辖区内现有居民3万人,请你估计这3万人中喜欢玉兰树的有多少人?

分析 (1)用桂花树的人数除以其占总人数的百分比可得;
(2)用360度乘以样本中枫树所占比例即可得;
(3)用总人数乘以样本中玉兰树所占比例即可得.
解答 解:(1)这次参与调查的居民人数为75÷37.5%=200(人),
故答案为:200;
(2)扇形统计图中“枫树”所在扇形的圆心角度数为360°×$\frac{20}{200}$=36°,
故答案为:36°;
(3)3×$\frac{200-(50+75+25+20)}{200}$=0.45(万人),
答:估计这3万人中喜欢玉兰树的有0.45万人.
点评 本题主要考查了条形图和扇形图,在解题时要注意灵活应用条形图和扇形图之间的关系是本题的关键.

练习册系列答案
相关题目
20.阅读下列材料,完成相应任务:
学习任务:
(1)将剩余部分的证明过程补充完整;
(2)若将图(1)中的点S与点D重合,重复材料中的操作过程得到图(4),请利用图(4),直接写出tan15°=2-$\sqrt{3}$(不必化简)
| 折纸三等分角 三等分角问题(trisection of an angle)是二千四百年前,古希腊人提出的几何三大作图问题之一(三等分任意角、化圆为方、倍立方),即用圆规与直尺(没有刻度,只能做直线的尺子)把一任意角三等分,这问题曾吸引着许多人去研究,但无一成功.1837年法国数学家凡齐尔(1814~1848)运用代数方法证明了,仅用尺规不可鞥呢三等分角. 如果作图工具没有限制,将条件放宽,将任意角三等分是可以解决的.下面介绍一种折纸三等分任意锐角的方法: (1)在正方形纸片上折出任意∠SBC,将正方形ABCD对折,折痕为记为MN,再将矩形MBCN对折,折痕记为EF,得到图(1); (2)翻折左下角使点B与EF上的点T重合,点M与SB上的点P重合,点E对折后的对应点记为Q,折痕为记为GH,得到图(2); (3)折出射线BQ,BT,得到图(3),则射线BQ,BT就是∠SBC的三等分线.  下面是证明BQ,BT是∠SBC三等分线的部分过程: 证明:过T作TK⊥BC,垂足为K,则四边形EBKT为矩形 根据折叠,得EB=QT,∠EBT=∠QTB,BT=TB ∴△EBT≌△QTB, ∴∠BQT=∠TEB=90°, ∴BQ⊥PT … |
(1)将剩余部分的证明过程补充完整;
(2)若将图(1)中的点S与点D重合,重复材料中的操作过程得到图(4),请利用图(4),直接写出tan15°=2-$\sqrt{3}$(不必化简)
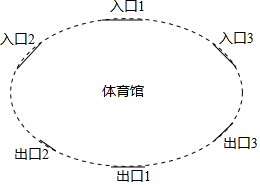 某体育馆有3个入口和3个出口,其示意图如下,参观者可从任意一个入口进入,参观结束后从任意一个出口离开
某体育馆有3个入口和3个出口,其示意图如下,参观者可从任意一个入口进入,参观结束后从任意一个出口离开

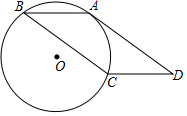 如图,?ABCD的边AD与经过A,B,C三点的⊙O相切,sin∠D=$\frac{5}{13}$,AD=24,则⊙O的半径为$\frac{169}{10}$.
如图,?ABCD的边AD与经过A,B,C三点的⊙O相切,sin∠D=$\frac{5}{13}$,AD=24,则⊙O的半径为$\frac{169}{10}$.
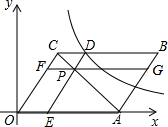 如图,在平面直角坐标系中,O为坐标原点,?OABC的边OA落在x轴正半轴上,顶点C(3,4),点P为对角线AC上一点,过点P分别作DE∥OC,FG∥OA分别交?OABC各边如图所示,反比例函数y=$\frac{k}{x}$图象过点D.
如图,在平面直角坐标系中,O为坐标原点,?OABC的边OA落在x轴正半轴上,顶点C(3,4),点P为对角线AC上一点,过点P分别作DE∥OC,FG∥OA分别交?OABC各边如图所示,反比例函数y=$\frac{k}{x}$图象过点D.