题目内容
16.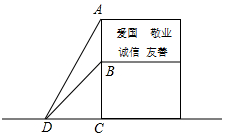 为了弘扬“社会主义核心价值观”,区政府在广场上竖立了如图所示的公益广告牌,并在两侧加固钢缆,已知钢缆底端D到达广告牌立柱AC的距离为5米,从点D测得广告牌顶端A点和底端B点的仰角分别为60°和45°,求广告牌的高度AB.
为了弘扬“社会主义核心价值观”,区政府在广场上竖立了如图所示的公益广告牌,并在两侧加固钢缆,已知钢缆底端D到达广告牌立柱AC的距离为5米,从点D测得广告牌顶端A点和底端B点的仰角分别为60°和45°,求广告牌的高度AB.
分析 根据已知和tan∠ADC=$\frac{AC}{DC}$,求出AC,根据∠BDC=45°,求出BC,根据AB=AC-BC求出AB.
解答 解:在Rt△ADC中,∵∠ADC=60°,CD=5米,
∵tan∠ADC=$\frac{AC}{DC}$,
∴AC=5•tan60°=5$\sqrt{3}$,
在Rt△BDC中,∵∠BDC=45°,
∴BC=CD=5,
∴AB=AC-BC=5($\sqrt{3}$-1)米.
点评 本题考查的是解直角三角形的知识,掌握仰角的概念和锐角三角函数的概念是解题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
6.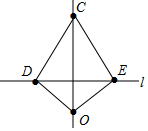 如图所示的仪器中,OD=OE,CD=CE.小州把这个仪器往直线l上一放,使点D、E落在直线l上,作直线OC,则OC⊥l,他这样判断的理由是( )
如图所示的仪器中,OD=OE,CD=CE.小州把这个仪器往直线l上一放,使点D、E落在直线l上,作直线OC,则OC⊥l,他这样判断的理由是( )
 如图所示的仪器中,OD=OE,CD=CE.小州把这个仪器往直线l上一放,使点D、E落在直线l上,作直线OC,则OC⊥l,他这样判断的理由是( )
如图所示的仪器中,OD=OE,CD=CE.小州把这个仪器往直线l上一放,使点D、E落在直线l上,作直线OC,则OC⊥l,他这样判断的理由是( )| A. | 到一个角两边距离相等的点在这个角的角平分线上 | |
| B. | 角平分线上的点到这个角两边的距离相等 | |
| C. | 到线段两端距离相等的点在这条线段的垂直平分线上 | |
| D. | 线段垂直平分线上的点到线段两端的距离相等 |
7.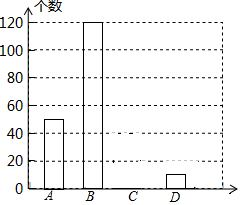 网上购物已经成为人们常用的一种购物方式,售后评价特别引人关注,为了解市民对售后评价的关注情况,随机采访部分市民,对采访情况制作了如下统计图表:
网上购物已经成为人们常用的一种购物方式,售后评价特别引人关注,为了解市民对售后评价的关注情况,随机采访部分市民,对采访情况制作了如下统计图表:
(1)根据上述统计图可得此次采访的人数为200人,a=20,b=0.25;
(2)根据以上信息补全条形统计图;
(3)根据上述采访结果,请估计在6400名市民中,高度关注售后评价的市民约有多少人?
 网上购物已经成为人们常用的一种购物方式,售后评价特别引人关注,为了解市民对售后评价的关注情况,随机采访部分市民,对采访情况制作了如下统计图表:
网上购物已经成为人们常用的一种购物方式,售后评价特别引人关注,为了解市民对售后评价的关注情况,随机采访部分市民,对采访情况制作了如下统计图表:| 关注情况 | 频数 | 频率 |
| A.高度关注 | 50 | b |
| B.一般关注 | 120 | 0.6 |
| C.不关注 | a | 0.1 |
| D.不知道 | 10 | 0.05 |
(2)根据以上信息补全条形统计图;
(3)根据上述采访结果,请估计在6400名市民中,高度关注售后评价的市民约有多少人?
11. 如图,△ABC 中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.
如图,△ABC 中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.
(1)求证:DF是⊙O的切线;
(2)若AC=3AE,写出求tanC的思路.
 如图,△ABC 中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.
如图,△ABC 中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.(1)求证:DF是⊙O的切线;
(2)若AC=3AE,写出求tanC的思路.
8.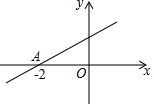 如图,直线y=kx+b与x轴的交点为A(-2,0),则不等式kx+b>0的解集为( )
如图,直线y=kx+b与x轴的交点为A(-2,0),则不等式kx+b>0的解集为( )
 如图,直线y=kx+b与x轴的交点为A(-2,0),则不等式kx+b>0的解集为( )
如图,直线y=kx+b与x轴的交点为A(-2,0),则不等式kx+b>0的解集为( )| A. | x>2 | B. | x≤2 | C. | x>-2 | D. | x≤-2 |
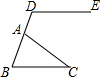 如图,△ABC中,点D在BA的延长线上,DE∥BC,如果∠BAC=65°,∠C=30°,那么∠BDE的度数是95°.
如图,△ABC中,点D在BA的延长线上,DE∥BC,如果∠BAC=65°,∠C=30°,那么∠BDE的度数是95°.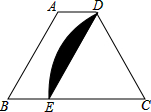 如图,四边形ABED是平行四边形,B、E、C三点共线,以点C为圆心,CDWie半径的弧与BC交于点E,AB=CD=4,则阴影部分的面积是$\frac{8}{3}$π-4$\sqrt{3}$.
如图,四边形ABED是平行四边形,B、E、C三点共线,以点C为圆心,CDWie半径的弧与BC交于点E,AB=CD=4,则阴影部分的面积是$\frac{8}{3}$π-4$\sqrt{3}$.