题目内容
1. 如图所示,△ABC的内角∠ABC的平分线与外角∠ACD的平分线相交于点A1,试探索∠A与∠A1的度数关系.
如图所示,△ABC的内角∠ABC的平分线与外角∠ACD的平分线相交于点A1,试探索∠A与∠A1的度数关系.
分析 根据角平分线的定义可得∠CBA1=$\frac{1}{2}$∠ABC,根据三角形的一个外角等于与它不相邻的两个内角的和和角平分线的定义表示出∠DCA1,然后整理即可得到∠A1=$\frac{1}{2}$∠A,代入数据计算即可得解.
解答 解:∵BA1平分∠ABC,
∴∠CBA1=$\frac{1}{2}$∠ABC,
∵CA1平分△ABC的外角,
∴∠DCA1=$\frac{1}{2}$∠ACD=$\frac{1}{2}$(∠A+∠ABC)=$\frac{1}{2}$∠A+$\frac{1}{2}$∠ABC,
在△BCA1中,由三角形的外角性质,∠DCA1=∠CBA1+∠A1=$\frac{1}{2}$∠ABC+∠A1,
∴$\frac{1}{2}$∠A+$\frac{1}{2}$∠ABC=$\frac{1}{2}$∠ABC+∠A1,
∴∠A1=$\frac{1}{2}$∠A.
点评 本题考查了三角形的外角性质的应用,能正确运用性质进行推理和计算是解此题的关键,注意:三角形的一个外角等于和它不相邻的两个内角的和.

练习册系列答案
相关题目
11.一组数据的最大值为105,最小值为23,若确定组距为9,则分成的组数为( )
| A. | 11 | B. | 10 | C. | 9 | D. | 8 |
9. 如图,为估计荔香公园小池塘岸边A、B两点之间的距离,小明在小池塘的一侧选取一点O,测得OA=15m,OB=10m,则A、B间的距离可能是( )
如图,为估计荔香公园小池塘岸边A、B两点之间的距离,小明在小池塘的一侧选取一点O,测得OA=15m,OB=10m,则A、B间的距离可能是( )
 如图,为估计荔香公园小池塘岸边A、B两点之间的距离,小明在小池塘的一侧选取一点O,测得OA=15m,OB=10m,则A、B间的距离可能是( )
如图,为估计荔香公园小池塘岸边A、B两点之间的距离,小明在小池塘的一侧选取一点O,测得OA=15m,OB=10m,则A、B间的距离可能是( )| A. | 5 m | B. | 15 m | C. | 25 m | D. | 30 m |
11.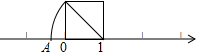 如图,以数轴的单位长度线段为边作一个正方形,以表示数1的点为圆心,正方形对角线长为半径画弧,交数轴于点A,则点A表示的数是( )
如图,以数轴的单位长度线段为边作一个正方形,以表示数1的点为圆心,正方形对角线长为半径画弧,交数轴于点A,则点A表示的数是( )
 如图,以数轴的单位长度线段为边作一个正方形,以表示数1的点为圆心,正方形对角线长为半径画弧,交数轴于点A,则点A表示的数是( )
如图,以数轴的单位长度线段为边作一个正方形,以表示数1的点为圆心,正方形对角线长为半径画弧,交数轴于点A,则点A表示的数是( )| A. | -$\sqrt{2}$ | B. | 1-$\sqrt{2}$ | C. | -1-$\sqrt{2}$ | D. | -1+$\sqrt{2}$ |
 我们知道有两条边相等的三角形叫做等腰三角形.类似的,我们定义:至少有一组对边相等的四边形叫做等对边四边形.
我们知道有两条边相等的三角形叫做等腰三角形.类似的,我们定义:至少有一组对边相等的四边形叫做等对边四边形.