题目内容
10.在等腰直角△ABC中,AC=BC,∠ACB=90°,CF⊥AB交AB于点F,点D在AC上,连接BD,交CF于点G,过点C作BD的垂线交BC于点H,交AB于点E:(1)如图1,∠ABD=∠CBD,CG=1,求AB;
(2)如图2,连接AH、FH,∠AHF=90°,求证:HB=$\sqrt{2}$AH.

分析 (1)如图1中,连接DE.由△BDC≌△BDE,推出CD=DE,∠DEB=∠DCB=90°,再证明∠CDG=∠CGD,推出CG=CD=DE=1,推出AD=$\sqrt{2}$,AC=$\sqrt{2}$+1,即可推出AB=$\sqrt{2}$AC=2+$\sqrt{2}$;
(2)如图2中,作AM⊥CE于M.首先证明△AMH是等腰直角三角形,推出AM=MH,再证明△ACM≌△CBH,推出BH=CM,CH=AM=HM,即可证明BH=2AM=$\sqrt{2}$AH.
解答 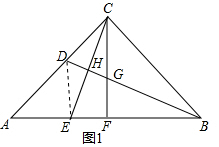 (1)解:如图1中,连接DE.
(1)解:如图1中,连接DE.
∵CE⊥BD,
∴∠BHC=∠BHE=90°,∵BH=BH,∠HBC=∠HBE,
∴△BHC≌△BHE,
∴BE=BC,∵∠DBC=∠DBE,BD=BD,
∴△BDC≌△BDE,
∴CD=DE,∠DEB=∠DCB=90°,
∵CA=CB,∠ACB=90°,CF⊥⊥AB,
∴∠A=∠BCF=45°,
∵∠CDB=∠A+∠ABD,∠CGD=∠BCG+∠CBD,
∴∠CDG=∠CGD,
∴CG=CD=DE=1,
∴AD=$\sqrt{2}$,AC=$\sqrt{2}$+1,
AB═$\sqrt{2}$AC=2+$\sqrt{2}$.
(2)证明:如图2中,作AM⊥CE于M.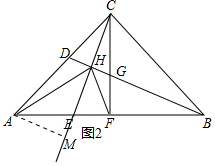 ∵∠EFC=∠EHB=90°,∠BEH=∠CEF,
∵∠EFC=∠EHB=90°,∠BEH=∠CEF,
∴△BHE∽△CFE,
∴$\frac{EH}{EF}$=$\frac{EB}{CE}$,
∴$\frac{EH}{EB}$=$\frac{EF}{EC}$,
∴△EHF∽△EBC,
∴∠EHF=∠EBC=45°,
∵∠AHF=90°,
∴∠AHM=45°,
∵∠AMH=90°,
∴△AMH是等腰直角三角形,
∴AM=MH,
∵AC=BC,∠ACM=∠CBH,∠AMC=∠BHC=90°,
∴△ACM≌△CBH,
∴BH=CM,CH=AM=HM,
∴BH=2AM=$\sqrt{2}$AH.
点评 本题考查全等三角形的判定和性质、等腰直角三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.

 如图所示,△ABC的内角∠ABC的平分线与外角∠ACD的平分线相交于点A1,试探索∠A与∠A1的度数关系.
如图所示,△ABC的内角∠ABC的平分线与外角∠ACD的平分线相交于点A1,试探索∠A与∠A1的度数关系. 如图,矩形ABCD的对角线AC、BD相交于点O,OF⊥AC于点O,交AB于E,交CB的延长线于点F,求证:AO2=OE•OF.
如图,矩形ABCD的对角线AC、BD相交于点O,OF⊥AC于点O,交AB于E,交CB的延长线于点F,求证:AO2=OE•OF. 如图,将线段AB放在每个小正方形的边长为1的网格中,点A、B均落在格点上,则线段AB的长为$\sqrt{26}$.
如图,将线段AB放在每个小正方形的边长为1的网格中,点A、B均落在格点上,则线段AB的长为$\sqrt{26}$.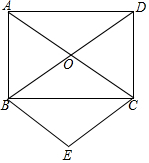 如图,矩形ABCD的对角线AC,BD相交于点O,∠ACB=30°,BC=3,分别过点B,C作BE∥AC,CE∥BD,且BE,CE相交于点E.
如图,矩形ABCD的对角线AC,BD相交于点O,∠ACB=30°,BC=3,分别过点B,C作BE∥AC,CE∥BD,且BE,CE相交于点E.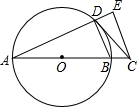 如图,AB为⊙O的直径,CD切⊙O于点D,交AB的延长线于点C,CE⊥AD于点E.
如图,AB为⊙O的直径,CD切⊙O于点D,交AB的延长线于点C,CE⊥AD于点E.