题目内容
13.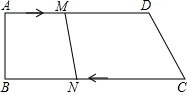 如图,已知四边形ABCD中,AD∥BC,∠B=90°,AD=25cm,CD=15cm,BC=35cm.动点M在AD边上以2cm/秒的速度由A向D运动;动点N在CB上以3cm/秒的速度由C向B运动,若点M,N分别从A,C同时出发,当其中一点到达端点时,另一点也随之停止运动,假设运动时间为t秒,问:
如图,已知四边形ABCD中,AD∥BC,∠B=90°,AD=25cm,CD=15cm,BC=35cm.动点M在AD边上以2cm/秒的速度由A向D运动;动点N在CB上以3cm/秒的速度由C向B运动,若点M,N分别从A,C同时出发,当其中一点到达端点时,另一点也随之停止运动,假设运动时间为t秒,问:(1)当四边形ABNM是矩形时,求出t的值;
(2)在某一时刻,是否存在MN=CD?若存在,则求出t的值;若不存在,说明理由.
分析 (1)四边形ABNM为矩形,即AM=BN,列出等式,求解即可;
(2)①如果MN=CD,即四边形MNCD为平行四边形,即MD=CN,列出等式求解;②四边形MNCD为等腰梯形,即CD=MN,过点M作MF⊥BC于F,根据勾股定理列出等式即可得出.
解答  解:∵设运动时间为t秒,
解:∵设运动时间为t秒,
∴AM=2t(cm),MD=AD-AM=25-2t(cm),CN=3t(cm),BN=BC-CN=35-3t(cm),
(1)如图1:∵AD∥BC,
∴当MA=BN时,四边形ABNM是平行四边形,
∵∠B=90°,
∴四边形ABNM是矩形,
即2t=35-3t,
解得:t=7,
∴t=7s时,四边形ABNM是矩形,
(2)①∵AD∥BC,
∴当四边形MNCD是平行四边形时,MN=CD,
此时有MD=CN,即3t=25-2t,
解得t=5.
∴当t=5s时,MN=CD;
②当四边形PQCD为等腰梯形时,MN=CD,
如图所示:
在Rt△MNF和Rt△CDE中,
∵MN=DC,MF=DE,
在Rt△MNF与Rt△CDE中,
$\left\{\begin{array}{l}{MN=DC}\\{MF=DE}\end{array}\right.$,
∴Rt△MNF≌Rt△CDE(HL),
∴NF=CE,
∴NC-MD=NC-EFNQF+EC=2CE,即3t-(25-2t)=20,
解得:t=9(s)
即当t=9(s)时,四边形PQCD为等腰梯形,此时MN=CD,
∴当t=5或t=9(s)时,MN=CD.
点评 此题主要考查了矩形、平行四边形、等腰梯形的判定与性质应用,根据题意画出图形是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,AB∥CD,∠1=110°,∠2=40°,则∠3=110°.
如图,AB∥CD,∠1=110°,∠2=40°,则∠3=110°.

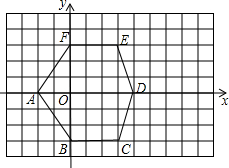 观察图,并回答一下问题:
观察图,并回答一下问题: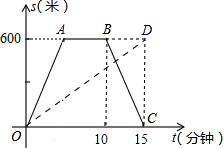 甲、乙二人沿同条路从学校出发去科技馆,甲骑自行车,乙步行,当甲以原速从原路回答学校时,乙刚好到达科技馆.图中折线O→A→B→C和线段OD分别表示他们离学校的路程y(米)与时间x(分)间的函数关系,则下列结论中正确的个数有( )
甲、乙二人沿同条路从学校出发去科技馆,甲骑自行车,乙步行,当甲以原速从原路回答学校时,乙刚好到达科技馆.图中折线O→A→B→C和线段OD分别表示他们离学校的路程y(米)与时间x(分)间的函数关系,则下列结论中正确的个数有( )
 如图,正方形ABCD中,AB=2,AC,BD交于点O.若E,F分别是边AB,BC上的动点,且OE⊥OF,则△OEF周长的最小值是2+$\sqrt{2}$.
如图,正方形ABCD中,AB=2,AC,BD交于点O.若E,F分别是边AB,BC上的动点,且OE⊥OF,则△OEF周长的最小值是2+$\sqrt{2}$.