题目内容
5.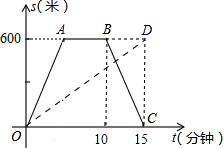 甲、乙二人沿同条路从学校出发去科技馆,甲骑自行车,乙步行,当甲以原速从原路回答学校时,乙刚好到达科技馆.图中折线O→A→B→C和线段OD分别表示他们离学校的路程y(米)与时间x(分)间的函数关系,则下列结论中正确的个数有( )
甲、乙二人沿同条路从学校出发去科技馆,甲骑自行车,乙步行,当甲以原速从原路回答学校时,乙刚好到达科技馆.图中折线O→A→B→C和线段OD分别表示他们离学校的路程y(米)与时间x(分)间的函数关系,则下列结论中正确的个数有( )(1)学校与科技馆的路程是600米;
(2)甲在科技馆停留的时间为5分钟;
(3)甲骑车的速度为120米/分钟;
(4)甲与乙迎面相遇时离学校500米;
(5)甲到达科技馆时乙才走了200米.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 观察图形,s的最大值即为学校与科技馆的路程;根据甲返回时的速度不变,用总时间15减去返回的时间的2倍,计算即可得解;用总路程除以返回的时间,计算即可得到速度;求出乙的速度,然后根据相遇时二人的路程之和等于总路程的二倍列出方程求出时间,再根据乙的步行速度进行计算即可得解.
解答 解:(1)s的最大值是600米,
所以学校与科技馆的路程是600米,故本结论正确;
(2)∵甲以原速从原路回到学校,
∴甲在科技馆查阅资料的时间为:10-(15-10)=5分钟,故本结论正确;
(3)甲骑车的速度=$\frac{600}{15-10}$=120米/分钟,故本结论正确;
(4)设乙出发t分钟两人相遇,
乙的速度=$\frac{600}{15}$=40米/分钟,
所以,40t+120×(t-5)=2×600,
解得t=$\frac{45}{4}$,
40×$\frac{45}{4}$=450米,
所以,相遇时距学校450米,故本结论错误.
(5)∵甲到达科技馆用时(15-10)=5分钟,
∴甲到达科技馆时乙走了40×5=200米,故本结论正确;
故选C.
点评 本题考查利用函数的图象解决实际问题,正确理解函数图象横纵坐标表示的意义,理解问题的过程,就能够通过图象得到函数问题的相应解决,D选项也可以利用求函数解析式的交点问题解答.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
16.甲、乙两人加工同一种玩具,甲加工90个玩具与乙加工120玩具所用的天数相同,已知甲、乙两人每天共加工35个玩具.若设甲每天加工x个玩具,则根据题意列方程( )
| A. | $\frac{120}{x}$=$\frac{90}{35-x}$ | B. | $\frac{90}{x}$=$\frac{120}{35+x}$ | C. | $\frac{90}{3x}$=$\frac{120}{35}$ | D. | $\frac{90}{x}$=$\frac{120}{35-x}$ |
17.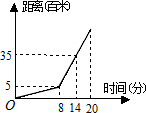 某天早上王文上学,先步行一段路,因时间紧,他又改乘出租车,结果到校时还是迟到了5分钟,其行程情况如图,若他出门时直接乘出租车(车速不变),则他( )
某天早上王文上学,先步行一段路,因时间紧,他又改乘出租车,结果到校时还是迟到了5分钟,其行程情况如图,若他出门时直接乘出租车(车速不变),则他( )
 某天早上王文上学,先步行一段路,因时间紧,他又改乘出租车,结果到校时还是迟到了5分钟,其行程情况如图,若他出门时直接乘出租车(车速不变),则他( )
某天早上王文上学,先步行一段路,因时间紧,他又改乘出租车,结果到校时还是迟到了5分钟,其行程情况如图,若他出门时直接乘出租车(车速不变),则他( )| A. | 仍会迟到2分钟到校 | B. | 刚好按时到校 | ||
| C. | 可以提前2分钟到校 | D. | 可以提前5分钟到校 |
 如图,在长20米,宽10米的长方形草地内修建了宽2米的道路,则草地的面积为144米2.
如图,在长20米,宽10米的长方形草地内修建了宽2米的道路,则草地的面积为144米2.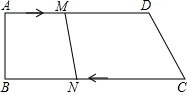 如图,已知四边形ABCD中,AD∥BC,∠B=90°,AD=25cm,CD=15cm,BC=35cm.动点M在AD边上以2cm/秒的速度由A向D运动;动点N在CB上以3cm/秒的速度由C向B运动,若点M,N分别从A,C同时出发,当其中一点到达端点时,另一点也随之停止运动,假设运动时间为t秒,问:
如图,已知四边形ABCD中,AD∥BC,∠B=90°,AD=25cm,CD=15cm,BC=35cm.动点M在AD边上以2cm/秒的速度由A向D运动;动点N在CB上以3cm/秒的速度由C向B运动,若点M,N分别从A,C同时出发,当其中一点到达端点时,另一点也随之停止运动,假设运动时间为t秒,问: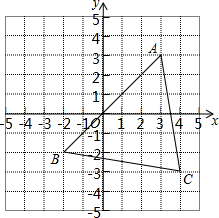 在如图所示的正方形网格中,每个小正方形的单位长度均为1,△ABC的三个顶点恰好是正方形网格的格点.
在如图所示的正方形网格中,每个小正方形的单位长度均为1,△ABC的三个顶点恰好是正方形网格的格点.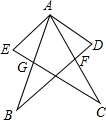 如图,在△ABD和△ACE中,F是AC和DB的交点,G是AB和EC的交点,现有如下4个论断:①AB=AC;②AD=AE;③AF=AG;④AD⊥BD,AE⊥CE.请以其中3个论断为已知条件,1个论断作为结论组成一个正确的说法,并证明其正确性.
如图,在△ABD和△ACE中,F是AC和DB的交点,G是AB和EC的交点,现有如下4个论断:①AB=AC;②AD=AE;③AF=AG;④AD⊥BD,AE⊥CE.请以其中3个论断为已知条件,1个论断作为结论组成一个正确的说法,并证明其正确性.