题目内容
4．
如图，AB∥CD，∠1=110°，∠2=40°，则∠3=110°．
分析 如图设∠2顶点为E，延长AE交DC的延长线于点F，由平行线的性质可求得∠F，在△CEF中利用三角形外角可求得∠3．
解答 解：
设∠2顶点为E，延长AE交DC的延长线于点F，如图，
∵AB∥CD，
∴∠F+∠1=180°，
∴∠F=180°-∠1=180°-110°=70°，
∵∠3是△CEF的一个外角，
∴∠3=∠2+∠F=40°+70°=110°，
故答案为：110°．
点评 本题主要考查平行线的性质，掌握平行线的性质是解题的关键，即①两直线平行，同位角相等，②两直线平行，内错角相等，③两直线平行，同旁内角互补．
练习册系列答案
阅读快车系列答案
相关题目
14．
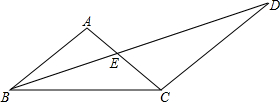如图，△ABC中AB=AC=10，BC=16．
（1）求△ABC的面积；
（2）若过点C作AB的平行线CD，并使CD=BC，连结BD，交AC于点E．探索∠ACB与∠D有怎样的数量关系？证明你的结论．
如图，△ABC中AB=AC=10，BC=16．（1）求△ABC的面积；
（2）若过点C作AB的平行线CD，并使CD=BC，连结BD，交AC于点E．探索∠ACB与∠D有怎样的数量关系？证明你的结论．
如图，在长20米，宽10米的长方形草地内修建了宽2米的道路，则草地的面积为144米2．
19．某校四个绿化小组某天的植树棵树如下：10，10，x，8．若这组数据的众数与平均数相等，那么这组数据的中位数是（ ）
| A． | 9 | B． | 10 | C． | 11 | D． | 12 |
16．甲、乙两人加工同一种玩具，甲加工90个玩具与乙加工120玩具所用的天数相同，已知甲、乙两人每天共加工35个玩具．若设甲每天加工x个玩具，则根据题意列方程（ ）
| A． | $\frac{120}{x}$=$\frac{90}{35-x}$ | B． | $\frac{90}{x}$=$\frac{120}{35+x}$ | C． | $\frac{90}{3x}$=$\frac{120}{35}$ | D． | $\frac{90}{x}$=$\frac{120}{35-x}$ |
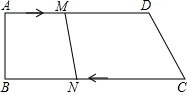如图，已知四边形ABCD中，AD∥BC，∠B=90°，AD=25cm，CD=15cm，BC=35cm．动点M在AD边上以2cm/秒的速度由A向D运动；动点N在CB上以3cm/秒的速度由C向B运动，若点M，N分别从A，C同时出发，当其中一点到达端点时，另一点也随之停止运动，假设运动时间为t秒，问：