题目内容
2.操作:准备一张长方形纸,按下图操作:(1)把矩形ABCD对折,得折痕MN;
(2)把A折向MN,得Rt△AEB;
(3)沿线段EA折叠,得到另一条折痕EF,展开后可得到△EBF.
探究:△EBF的形状,并说明理由.
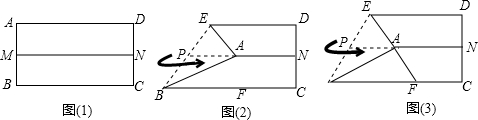
分析 由(1)得出M、N分别是AB、DC的中点,由(2)得出BE=2AP,再由(3)得出BF=2AP,证出BE=BF,因此∠1=∠2,由角的关系求出∠1=60°,即可证出△EBF为等边三角形.
解答 解:△EBF是等边三角形;理由如下:如图所示: 由操作(1)得:M、N分别是AB、DC的中点,
由操作(1)得:M、N分别是AB、DC的中点,
∴在Rt△ABE中,P为BE的中点,AP是斜边上的中线,
∴AP=BP=$\frac{1}{2}$BE,即BE=2AP,
在△EBF中,A是EF的中点,
∴AP=$\frac{1}{2}$BF,即BF=2AP,
∴BE=BF,
∴∠1=∠2,
又∵∠2=∠3,2∠1+∠3=180°,
∴3∠1=180°,
∴∠1=60°,
∴△EBF为等边三角形.
点评 本题考查了矩形的性质、翻折变换的性质、直角三角形斜边上的中线性质、等边三角形的判定;熟练掌握翻折变换和矩形的性质,并能进行推理论证是解决问题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
17.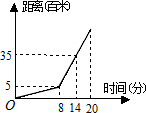 某天早上王文上学,先步行一段路,因时间紧,他又改乘出租车,结果到校时还是迟到了5分钟,其行程情况如图,若他出门时直接乘出租车(车速不变),则他( )
某天早上王文上学,先步行一段路,因时间紧,他又改乘出租车,结果到校时还是迟到了5分钟,其行程情况如图,若他出门时直接乘出租车(车速不变),则他( )
 某天早上王文上学,先步行一段路,因时间紧,他又改乘出租车,结果到校时还是迟到了5分钟,其行程情况如图,若他出门时直接乘出租车(车速不变),则他( )
某天早上王文上学,先步行一段路,因时间紧,他又改乘出租车,结果到校时还是迟到了5分钟,其行程情况如图,若他出门时直接乘出租车(车速不变),则他( )| A. | 仍会迟到2分钟到校 | B. | 刚好按时到校 | ||
| C. | 可以提前2分钟到校 | D. | 可以提前5分钟到校 |
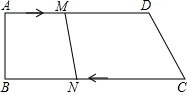 如图,已知四边形ABCD中,AD∥BC,∠B=90°,AD=25cm,CD=15cm,BC=35cm.动点M在AD边上以2cm/秒的速度由A向D运动;动点N在CB上以3cm/秒的速度由C向B运动,若点M,N分别从A,C同时出发,当其中一点到达端点时,另一点也随之停止运动,假设运动时间为t秒,问:
如图,已知四边形ABCD中,AD∥BC,∠B=90°,AD=25cm,CD=15cm,BC=35cm.动点M在AD边上以2cm/秒的速度由A向D运动;动点N在CB上以3cm/秒的速度由C向B运动,若点M,N分别从A,C同时出发,当其中一点到达端点时,另一点也随之停止运动,假设运动时间为t秒,问: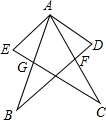 如图,在△ABD和△ACE中,F是AC和DB的交点,G是AB和EC的交点,现有如下4个论断:①AB=AC;②AD=AE;③AF=AG;④AD⊥BD,AE⊥CE.请以其中3个论断为已知条件,1个论断作为结论组成一个正确的说法,并证明其正确性.
如图,在△ABD和△ACE中,F是AC和DB的交点,G是AB和EC的交点,现有如下4个论断:①AB=AC;②AD=AE;③AF=AG;④AD⊥BD,AE⊥CE.请以其中3个论断为已知条件,1个论断作为结论组成一个正确的说法,并证明其正确性.