题目内容
3. 如图,正方形ABCD中,AB=2,AC,BD交于点O.若E,F分别是边AB,BC上的动点,且OE⊥OF,则△OEF周长的最小值是2+$\sqrt{2}$.
如图,正方形ABCD中,AB=2,AC,BD交于点O.若E,F分别是边AB,BC上的动点,且OE⊥OF,则△OEF周长的最小值是2+$\sqrt{2}$.
分析 根据正方形的对角线互相平分且相等可得AO=BO,∠AOB=90°,对角线平分一组对角可得∠OAE=∠OBF,再根据AE=BF,然后利用“SAS”证明△AOE和△BOF全等,根据全等三角形对应角相等可得∠AOE=∠BOF,可得∠EOF=90°,然后利用勾股定理列式计算即可得解.
解答 解:在正方形ABCD中,AO=BO,∠AOB=90°,∠OAE=∠OBF=45°,
∵点E、F的速度相等,
∴AE=BF,
在△AOE和△BOF中,
$\left\{\begin{array}{l}{OA=BO}\\{∠OAE=∠OBF}\\{AE=BF}\end{array}\right.$,
∴△AOE≌△BOF(SAS),
∴∠AOE=∠BOF,
∴∠AOE+∠BOE=90°,
∴∠BOF+∠BOE=90°,
∴∠EOF=90°,
在Rt△BEF中,设AE=x,则BF=x,BE=2-x,
EF=$\sqrt{B{E}^{2}+B{F}^{2}}$=$\sqrt{(2-x)^{2}+{x}^{2}}$=$\sqrt{2(x-1)^{2}+2}$.
∴当x=1时,EF有最小值为$\sqrt{2}$.
∴OE=OF=1.
∴△OEF周长的最小值=2+$\sqrt{2}$.
故答案为:2$+\sqrt{2}$.
点评 本题考查了正方形的性质,全等三角形的判定与性质,同角的余角相等的性质,熟记正方形的性质,求出三角形全等的条件是解题的关键.

练习册系列答案
相关题目
18.己知反比例函数$y=\frac{m-2}{x}$(m为常数),当x>0时,y随x的增大而增大,则m的取值范围是( )
| A. | m>0 | B. | m>2 | C. | m<0 | D. | m<2 |
8.下列运算中,正确的是( )
| A. | a6÷a2=a3 | B. | a-6÷a-2=a-4 | C. | 6a2b÷2ab=3ab | D. | (2xy+y)÷y=2x+y |
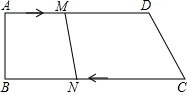 如图,已知四边形ABCD中,AD∥BC,∠B=90°,AD=25cm,CD=15cm,BC=35cm.动点M在AD边上以2cm/秒的速度由A向D运动;动点N在CB上以3cm/秒的速度由C向B运动,若点M,N分别从A,C同时出发,当其中一点到达端点时,另一点也随之停止运动,假设运动时间为t秒,问:
如图,已知四边形ABCD中,AD∥BC,∠B=90°,AD=25cm,CD=15cm,BC=35cm.动点M在AD边上以2cm/秒的速度由A向D运动;动点N在CB上以3cm/秒的速度由C向B运动,若点M,N分别从A,C同时出发,当其中一点到达端点时,另一点也随之停止运动,假设运动时间为t秒,问: