题目内容
6.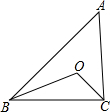 如图,△ABC中,O是∠ABC和∠ACB的角平分线的交点,若∠A=40°,则∠BOC=110°.
如图,△ABC中,O是∠ABC和∠ACB的角平分线的交点,若∠A=40°,则∠BOC=110°.
分析 求出∠ABC+∠ACB的度数,根据平分线的定义得出∠OBC=$\frac{1}{2}$∠ABC,∠OCB=$\frac{1}{2}$∠ACB,求出∠OBC+∠OCB的度数,根据三角形内角和定理求出即可.
解答 解:∵∠A=40°,
∴∠ABC+∠ACB=180°-∠A=140°,
∵BO、CO分别是△ABC的角∠ABC、∠ACB的平分线,
∴∠OBC=$\frac{1}{2}$∠ABC,∠OCB=$\frac{1}{2}$∠ACB,
∴∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠ACB)=70°,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-70°=110°,
故答案为:110.
点评 本题考查了三角形内角和定理,角平分线定义的应用,注意:三角形的内角和等于180°.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.笼中有x只鸡y只兔,共有36只脚,能表示题中数量关系的方程是( )
| A. | x+y=18 | B. | x+y=36 | C. | 4x+2y=36 | D. | 2x+4y=36 |
18.将6个边长是1的正方形无缝隙铺成一个矩形,则这个矩形的对角线长等于( )
| A. | $\sqrt{37}$ | B. | $\sqrt{13}$ | C. | $\sqrt{37}$、$\sqrt{13}$ | D. | $\sqrt{37}$、$\sqrt{13}$、5 |
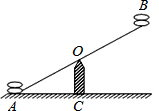 如图是跷跷板示意图,横板AB绕中点O上下转动,立柱OC与地面垂直,当横板AB的A端着地时,测得∠OAC=α,则在玩跷跷板时,横板AB绕点O上下转动的最大角度为2α°.
如图是跷跷板示意图,横板AB绕中点O上下转动,立柱OC与地面垂直,当横板AB的A端着地时,测得∠OAC=α,则在玩跷跷板时,横板AB绕点O上下转动的最大角度为2α°.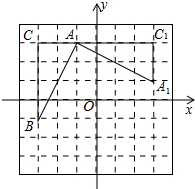 如图,在平面直角坐标系中,有一Rt△ABC,且A(-1,3),B(-3,-1),C(-3,3),已知△A1AC1是由△ABC旋转得到的.
如图,在平面直角坐标系中,有一Rt△ABC,且A(-1,3),B(-3,-1),C(-3,3),已知△A1AC1是由△ABC旋转得到的.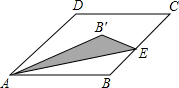 如图,已知在周长为20的菱形ABCD中,∠C=45°,点E是线段BC上一点,将△ABE沿AE所在直线翻折,使点B落在B′上,则在点E沿B→C→D运动的过程中,点B′运动的路径长是$\frac{5π}{4}$.
如图,已知在周长为20的菱形ABCD中,∠C=45°,点E是线段BC上一点,将△ABE沿AE所在直线翻折,使点B落在B′上,则在点E沿B→C→D运动的过程中,点B′运动的路径长是$\frac{5π}{4}$.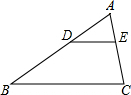 如图,在△ABC中,DE∥BC,$\frac{AD}{AB}=\frac{1}{3}$,DE=6,则BC的长是18.
如图,在△ABC中,DE∥BC,$\frac{AD}{AB}=\frac{1}{3}$,DE=6,则BC的长是18.