题目内容
15.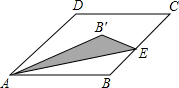 如图,已知在周长为20的菱形ABCD中,∠C=45°,点E是线段BC上一点,将△ABE沿AE所在直线翻折,使点B落在B′上,则在点E沿B→C→D运动的过程中,点B′运动的路径长是$\frac{5π}{4}$.
如图,已知在周长为20的菱形ABCD中,∠C=45°,点E是线段BC上一点,将△ABE沿AE所在直线翻折,使点B落在B′上,则在点E沿B→C→D运动的过程中,点B′运动的路径长是$\frac{5π}{4}$.
分析 由菱形的性质求出菱形的边长AB,由题意得出点B′运动的路径长是以A为圆心,半径是AB,圆心角为∠BAD的弧长,代入弧长公式计算即可.
解答 解:根据题意得:AB′=AB,
∵四边形ABCD是菱形,
∴AB=BC=CD=DA,∠BAD=∠C=45°,
∵菱形ABCD的周长为20,
∴AB=5,
∴AB′=5,
在点E沿B→C→D运动的过程中,点B′运动的路径长是以A为圆心,半径是AB′,圆心角为∠BAD的弧长,
∴点B′运动的路径长=$\frac{45π×5}{180}$=$\frac{5π}{4}$;
故答案为:$\frac{5π}{4}$.
点评 本题考查了菱形的性质、翻折变换的性质、弧长公式;熟练掌握菱形和翻折变换的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
3.某大学生利用暑假开展了30天的社会实践活动,参与了某超市的经营,了解到某成本为10元/件的商品杂x天销售的相关信息,如表表示:
设该超市在第x天销售这种商品获得的利润为y元.
(1)求y关于x的函数关系式;
(2)在这30天中,该超市销售这种商品第几天的利润最大?最大利润是多少?
| 销售量p(件) | P=40-x |
| 销售单价q(元/件) | 当1≤x≤20时,q=20+x 当20<x≤30时,q=40 |
(1)求y关于x的函数关系式;
(2)在这30天中,该超市销售这种商品第几天的利润最大?最大利润是多少?
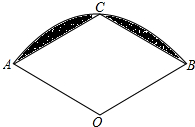 如图,在扇形AOB中,半径OA=2,∠AOB=120°,C为弧AB的中点,连接AC、BC,则图中阴影部分的面积是$\frac{4π}{3}$-2$\sqrt{3}$(结果保留π).
如图,在扇形AOB中,半径OA=2,∠AOB=120°,C为弧AB的中点,连接AC、BC,则图中阴影部分的面积是$\frac{4π}{3}$-2$\sqrt{3}$(结果保留π).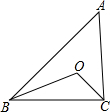 如图,△ABC中,O是∠ABC和∠ACB的角平分线的交点,若∠A=40°,则∠BOC=110°.
如图,△ABC中,O是∠ABC和∠ACB的角平分线的交点,若∠A=40°,则∠BOC=110°.
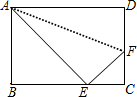 如图所示,将矩形ABCD沿直线AF折叠,点D恰好落在边BC上的点E处,若AB=8cm,BC=10cm,求EF的长.
如图所示,将矩形ABCD沿直线AF折叠,点D恰好落在边BC上的点E处,若AB=8cm,BC=10cm,求EF的长.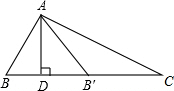 如图,△ABC中,∠B=2∠C,AD是BC上的高,沿AD所在直线将△ABD翻折,点B落在B′处.
如图,△ABC中,∠B=2∠C,AD是BC上的高,沿AD所在直线将△ABD翻折,点B落在B′处.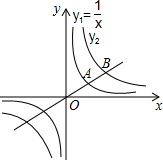 如图,过原点O的直线与反比例函数y1,y2的图象在第一象限内分别交于点A,B,且A为OB的中点,若函数y1=$\frac{1}{x}$,则y2与x的函数表达式是y2=$\frac{4}{x}$.
如图,过原点O的直线与反比例函数y1,y2的图象在第一象限内分别交于点A,B,且A为OB的中点,若函数y1=$\frac{1}{x}$,则y2与x的函数表达式是y2=$\frac{4}{x}$.