题目内容
18.将6个边长是1的正方形无缝隙铺成一个矩形,则这个矩形的对角线长等于( )| A. | $\sqrt{37}$ | B. | $\sqrt{13}$ | C. | $\sqrt{37}$、$\sqrt{13}$ | D. | $\sqrt{37}$、$\sqrt{13}$、5 |
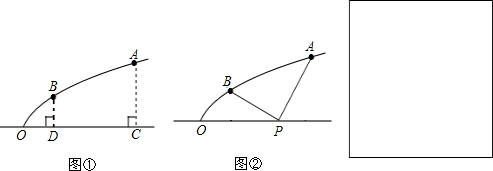
分析 如图1或图2所示,分类讨论,利用勾股定理可得结论.
解答 解:当如图1所示时,AB=2,BC=3,
∴AC=$\sqrt{{2}^{2}{+3}^{2}}$=$\sqrt{13}$;
当如图2所示时,AB=1,BC=6,
∴AC=$\sqrt{{1}^{2}{+6}^{2}}$=$\sqrt{37}$;
故选C.
点评 本题主要考查图形的拼接,数形结合,分类讨论是解答此题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
9.下列计算正确的是( )
| A. | 2a3+a3=3a6 | B. | (-2a4)4=16a8 | C. | (-a)6÷(-a)3=-a3 | D. | (a+1)2=a2+1 |
3.某大学生利用暑假开展了30天的社会实践活动,参与了某超市的经营,了解到某成本为10元/件的商品杂x天销售的相关信息,如表表示:
设该超市在第x天销售这种商品获得的利润为y元.
(1)求y关于x的函数关系式;
(2)在这30天中,该超市销售这种商品第几天的利润最大?最大利润是多少?
| 销售量p(件) | P=40-x |
| 销售单价q(元/件) | 当1≤x≤20时,q=20+x 当20<x≤30时,q=40 |
(1)求y关于x的函数关系式;
(2)在这30天中,该超市销售这种商品第几天的利润最大?最大利润是多少?
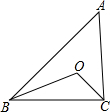 如图,△ABC中,O是∠ABC和∠ACB的角平分线的交点,若∠A=40°,则∠BOC=110°.
如图,△ABC中,O是∠ABC和∠ACB的角平分线的交点,若∠A=40°,则∠BOC=110°.
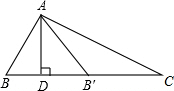 如图,△ABC中,∠B=2∠C,AD是BC上的高,沿AD所在直线将△ABD翻折,点B落在B′处.
如图,△ABC中,∠B=2∠C,AD是BC上的高,沿AD所在直线将△ABD翻折,点B落在B′处.