题目内容
9.在△ABC中,AB=7,BC=24,AC=25,则△ABC的面积是84.分析 首先利用勾股定理逆定理判定三角形是直角三角形,然后再利用三角形的面积公式计算出面积即可.
解答 解:∵72+242=252,
∴该三角形是直角三角形,
∴△ABC的面积是:$\frac{1}{2}$×24×7=84,
故答案为:84.
点评 本题考查勾股定理的逆定理的应用.关键是掌握勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
17.下列计算正确的是( )
| A. | $\sqrt{(-4)^2}$=-4 | B. | ($\sqrt{2}$)2=4 | C. | $\sqrt{5}$+$\sqrt{2}$=$\sqrt{7}$ | D. | $\sqrt{18}$÷$\sqrt{2}$=3 |
1.下列是二次根式的是( )
| A. | $\root{3}{2}$ | B. | $\sqrt{-2}$ | C. | $\sqrt{(-2)^{2}}$ | D. | $\sqrt{a}$ |
18.某学校号召同学们为灾区学生自愿捐款.已知第一次捐款总额为4800元,第二次捐款总额为5000元,第二次捐款人数比第一次多20人,而且两次人均捐款额恰好相等.如果设第一次捐款人数为x人,那么x满足的方程是( )
| A. | $\frac{4800}{x}=\frac{5000}{x-20}$ | B. | $\frac{4800}{x}=\frac{5000}{x+20}$ | C. | $\frac{4800}{x-20}=\frac{5000}{x}$ | D. | $\frac{4800}{x+20}=\frac{5000}{x}$ |
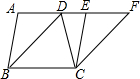 如图,在四边形ABCD中,AD∥BC,且AD<BC,连接BD,现将三角形ABD平移到三角形ECF的位置.
如图,在四边形ABCD中,AD∥BC,且AD<BC,连接BD,现将三角形ABD平移到三角形ECF的位置.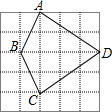 如图,5×5网格的每个小正方形的边长均为1,每个小正方形的顶点叫做格点,四边形ABCD的顶点A、B、C、D均在格点上,连接BD.
如图,5×5网格的每个小正方形的边长均为1,每个小正方形的顶点叫做格点,四边形ABCD的顶点A、B、C、D均在格点上,连接BD.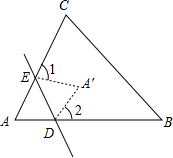 如图,在折纸活动中,小明制作了一张△ABC纸片,点D、E分别是边AB、AC上,将△ABC沿着DE折叠压平,A与A′重合,若∠A=68°,则∠1+∠2=136°.
如图,在折纸活动中,小明制作了一张△ABC纸片,点D、E分别是边AB、AC上,将△ABC沿着DE折叠压平,A与A′重合,若∠A=68°,则∠1+∠2=136°.