题目内容
8.如图1在平面直角坐标系中,点O为坐标原点,已知抛物线y=a(x+1)(x-3)与x轴相交于A、B两点(点A在点B的左侧),与y轴正半轴交于点C,且∠ABC=45°.(1)求a的值;
(2)如图2,点D在线段BC上(不与C重合),当AD=AC时,求D点坐标;
(3)如图3,在(2)的条件下,E为抛物线上一点,且在第一象限,过E作EF∥AD与AC相交于点F,当EF被BC平分时,求点E坐标.
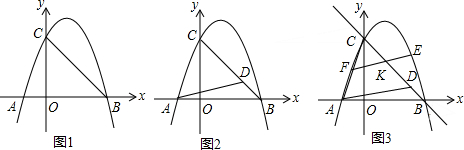
分析 (1)通过抛物线解析式求出点AB坐标,利用等腰直角三角形性质求出C点坐标,代入抛物线即可求出a值;
(2)由B、C点坐标可得出直线BC的解析式,设出D点坐标(m,-m+3),由两点间的距离公式可表示出AD的长度,再由AC=AD找出关于m的一元二次方程,解方程求出m的值,代入到D点坐标中即可得出结论.
(3)由A、D点坐标可得出直线AD的解析式,由EF平行AD设出直线EF的解析式,代入到抛物线中可得到关于x的一元二次方程,根据根与系数的关系表示出两根之和,再由直线EF和BC的解析式可找出交点的坐标,根据EF被BC平分,可知交点的横坐标的2倍为前面一元二次方程的两根之和,解方程即可得出直线EF的解析式,从而得出点E的坐标.
解答 解(1)抛物线y=a(x+1)(x-3),
令y=0,则有a(x+1)(x-3)=0,
解得:x=-1,或x=3,
∴A(-1,0),B(3,0),
∵∠ABC=45°,∠BOC=90°,
∴OB=OC=3,
∴C(0,3),
将点C(0,3)代入二次函数解析式得:
3=a×(0+1)×(0-3),
解得:a=-1.
(2)∵点A(-1,0),点C(0,3),点B(3,0),
∴AC=$\sqrt{10}$,
又∵∠ABC=45°,
∴直线BC的解析式为y=-x+3,
设点D的坐标为(m,-m+3),
由两点间的距离公式可知:AD=$\sqrt{[m-(-1)]^{2}+(-m+3)^{2}}$,
∵AD=AC=$\sqrt{10}$,
∴有$\sqrt{[m-(-1)]^{2}+(-m+3)^{2}}$=$\sqrt{10}$,
解得:m=0(舍去),m=2,
此时-m+3=-2+3=1.
故当AD=AC时,D点坐标为(2,1).
(3)设直线AD的解析式为y=kx+b,
将A(-1,0),D(2,1)代入,得
$\left\{\begin{array}{l}{0=-k+b}\\{1=2k+b}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=\frac{1}{3}}\\{b=\frac{1}{3}}\end{array}\right.$.
∴直线AD的解析式为y=$\frac{1}{3}$x+$\frac{1}{3}$.
∵EF∥AD,
∴设直线EF的解析式为y=$\frac{1}{3}$x+c.
令-x+3=$\frac{1}{3}$x+c,则有x=$\frac{3}{4}$(3-c).
将y=$\frac{1}{3}$x+c代入y=-1(x+1)(x-3)中,得
${x}^{2}-\frac{5}{3}x$-(3-c)=0,
由根与系数的关系可知:x1+x2=-$\frac{-\frac{5}{3}}{1}$=$\frac{5}{3}$.
∵EF被BC平分,
∴EF与BC的交点的横坐标为$\frac{{x}_{1}+{x}_{2}}{2}$,
即$\frac{3}{4}$(3-c)×2=$\frac{5}{3}$,解得:c=$\frac{17}{9}$.
解方程${x}^{2}-\frac{5}{3}x$-(3-$\frac{17}{9}$)=0,得:x1=$\frac{5-\sqrt{65}}{6}$,x2=$\frac{5+\sqrt{65}}{6}$.
∵点E在第一象限,
∴点E的横坐标为$\frac{5+\sqrt{65}}{6}$.
将x=$\frac{5+\sqrt{65}}{6}$代入y=$\frac{1}{3}$x+$\frac{17}{9}$中得,y=$\frac{39+\sqrt{65}}{18}$.
∴点E的坐标为($\frac{5+\sqrt{65}}{6}$,$\frac{39+\sqrt{65}}{18}$).
点评 本题考查了二次函数的应用、待定系数法求函数解析式、两点间的距离公式以及根与系数的关系,解题的关键:(1)找出C点的坐标;(2)用含m的代数式表示AD的长度;(3)由根与系数的关系结合中点坐标找出关于c的一元一次方程.本题属于中档题,(1)(2)没有难度;(3)难度不小,由于数据较大,带来运算的麻烦.解决该类题型时,联立直线与二次函数的关系式,利用根与系数的关系来表示出两根之和能给解题带来极大的方便.

 阅读快车系列答案
阅读快车系列答案| A. | a=1.5,b=2,c=3 | B. | a=3,b=4,c=5 | C. | a=6,b=8,c=10 | D. | a=7,b=24,c=25 |
| A. | $\sqrt{(-4)^2}$=-4 | B. | ($\sqrt{2}$)2=4 | C. | $\sqrt{5}$+$\sqrt{2}$=$\sqrt{7}$ | D. | $\sqrt{18}$÷$\sqrt{2}$=3 |
| A. | $\frac{4800}{x}=\frac{5000}{x-20}$ | B. | $\frac{4800}{x}=\frac{5000}{x+20}$ | C. | $\frac{4800}{x-20}=\frac{5000}{x}$ | D. | $\frac{4800}{x+20}=\frac{5000}{x}$ |
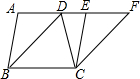 如图,在四边形ABCD中,AD∥BC,且AD<BC,连接BD,现将三角形ABD平移到三角形ECF的位置.
如图,在四边形ABCD中,AD∥BC,且AD<BC,连接BD,现将三角形ABD平移到三角形ECF的位置. 已知:如图,在?ABCD中,点E、F在AC上,且AE=CF.求证:四边形EBFD是平行四边形.
已知:如图,在?ABCD中,点E、F在AC上,且AE=CF.求证:四边形EBFD是平行四边形.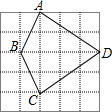 如图,5×5网格的每个小正方形的边长均为1,每个小正方形的顶点叫做格点,四边形ABCD的顶点A、B、C、D均在格点上,连接BD.
如图,5×5网格的每个小正方形的边长均为1,每个小正方形的顶点叫做格点,四边形ABCD的顶点A、B、C、D均在格点上,连接BD.