题目内容
7.定义:如果一个四边形中有一组邻边相等,且这两边夹角的对角被对角线平分,则称这个四边形为准对四边形,这条对角线为准对轴,被等分的角为准对角.如果一个准对四边形的准对角为60°,准对轴长为6,准对轴所对的一个角为120°,则这个四边形的面积为6$\sqrt{3}$.分析 只要证明四边形ABCD是菱形,求出对角线的长即可求面积.
解答 解;如图,四边形ABCD中,AD=AB,∠DAB=60°,CA平分∠DAB,AC=6,∠ABC=120°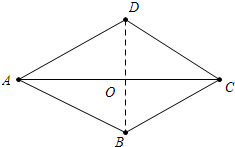 ,
,
∵AD=AB,∠DAB=60°,
∴△ABD是等边三角形,
∴∠ABD=∠ADB=60°,
在△ACD和△ACB中,
$\left\{\begin{array}{l}{AC=AC}\\{∠DAC=∠BAC}\\{AD=AB}\end{array}\right.$,
∴△ACD≌△ACB,
∴∠ADC=∠ABC=120°,
∴∠CBD=∠CDB=60°,
∴△CBD是等边三角形,
∴AD=CD=BC=AB,
∴四边形ABCD是菱形,
∴AC⊥BD,AO=OC=6,OD=OB,
在RT△AOD中,∵AO=3,∠DAO=30°,
∴DO=$\sqrt{3}$,
∴BD=2OD=2$\sqrt{3}$,
∴S菱形ABCD=$\frac{1}{2}$•AC•BD=$\frac{1}{2}$×$6×2\sqrt{3}$=6$\sqrt{3}$.
故答案为6$\sqrt{3}$.
点评 本题考查全等三角形的判定和性质、直角三角形30度角的性质、菱形的性质以及面积公式,解题的关键是确定四边形ABCD是菱形,利用特殊角解决问题,属于中考常考题型.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
12.已知∠BAC=90°,半径为r的圆O与两条直角边AB,AC都相切,设AB=a(a>r),BE与圆O相切于点E.现给出下列命题:①当∠ABE=60°时,BE=$\sqrt{3}r$; ②当∠ABE=90°时,BE=r;则下列判断正确的是( )
| A. | 命题①是真命题,命题②是假命题 | B. | 命题①②都是真命题 | ||
| C. | 命题①是假命题,命题②是真命题 | D. | 命题①②都是假命题 |
19.若线段CD是由线段AB平移得到的,点A(-1,3)的对应点为C(2,2),则点B(-3,-1)的对应点D的坐标是( )
| A. | (0,-2) | B. | (1,-2) | C. | (-2,0) | D. | (4,6) |
 实数a,b,c,d在数轴上的位置如图所示,|a|=|b|,化简:|b-a|-3|a+c|-|-b-c|+|d-c|.
实数a,b,c,d在数轴上的位置如图所示,|a|=|b|,化简:|b-a|-3|a+c|-|-b-c|+|d-c|. 如图,在平面直角坐标系xOy中,点A的坐标为(2,0),点B在第一象限内,OB=AB,且∠OBA=45°,点P是x轴正半轴上的一动点(点P在点A的右侧),以BP为腰作等腰△BPQ,且BP=BQ,∠PBQ=45°.已知点Q的坐标为(x,y),则y与x的函数关系式是y=x-2.
如图,在平面直角坐标系xOy中,点A的坐标为(2,0),点B在第一象限内,OB=AB,且∠OBA=45°,点P是x轴正半轴上的一动点(点P在点A的右侧),以BP为腰作等腰△BPQ,且BP=BQ,∠PBQ=45°.已知点Q的坐标为(x,y),则y与x的函数关系式是y=x-2.


