题目内容
二次函数y=ax2+bx+c的图象与x轴有两个交点,则对应的一元二次方程 ;如果只有一个交点,则对应的一元二次方程 ;如果没有交点,则对应的一元二次方程 ,因而抛物线与x轴的交点情况可由对应的一元二次方程的判别式予以判别.
考点:抛物线与x轴的交点
专题:
分析:利用求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标.即可得出二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的交点与一元二次方程ax2+bx+c=0根之间的关系,进而填空即可.
解答:解:二次函数y=ax2+bx+c的图象与x轴有两个交点,则对应的一元二次方程 有两个不相等的实数根;
如果只有一个交点,则对应的一元二次方程 有两个相等的实数根;
如果没有交点,则对应的一元二次方程 无实数根,
因而抛物线与x轴的交点情况可由对应的一元二次方程的判别式予以判别.
故答案为:有两个不相等的实数根;有两个相等的实数根;无实数根.
如果只有一个交点,则对应的一元二次方程 有两个相等的实数根;
如果没有交点,则对应的一元二次方程 无实数根,
因而抛物线与x轴的交点情况可由对应的一元二次方程的判别式予以判别.
故答案为:有两个不相等的实数根;有两个相等的实数根;无实数根.
点评:此题主要考查了抛物线与x轴的交点,正确掌握二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的交点与一元二次方程ax2+bx+c=0根之间的关系是解题关键.

练习册系列答案
相关题目
若抛物线y=ax2+bx+c(a<0)的顶点在第三象限,则一元二次方程ax2+bx+c=0的根的情况是( )
| A、有两个相等的实数根 |
| B、有两个不相等的实数根 |
| C、没有实数根 |
| D、无法确定 |
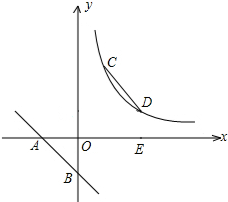 已知直线y=-2x-2交坐标轴于A,B两点,E为y轴上一点,线段AB沿AE方向平移到CD,反比例函数y=
已知直线y=-2x-2交坐标轴于A,B两点,E为y轴上一点,线段AB沿AE方向平移到CD,反比例函数y=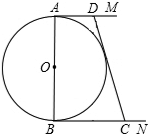 如图,⊙0的直径AB=2,AM和BN是它的两条切线,且AD+BC=CD,连OD,OC,
如图,⊙0的直径AB=2,AM和BN是它的两条切线,且AD+BC=CD,连OD,OC, 已知:如图,点C为线段AB上一点,BC=3cm,点D、点E分别为AC和AB的中点,则线段DE的长为
已知:如图,点C为线段AB上一点,BC=3cm,点D、点E分别为AC和AB的中点,则线段DE的长为