题目内容
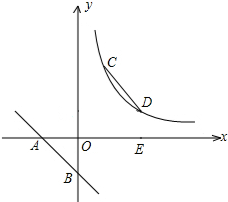 已知直线y=-2x-2交坐标轴于A,B两点,E为y轴上一点,线段AB沿AE方向平移到CD,反比例函数y=
已知直线y=-2x-2交坐标轴于A,B两点,E为y轴上一点,线段AB沿AE方向平移到CD,反比例函数y=| k |
| x |
考点:反比例函数综合题
专题:
分析:根据函数值,可得自变量的值,根据平移的性质,可得AB、DC、EF的关系,根据全等三角形的判定与性质,可得OE与OB的关系,根据线段中点的性质,可得C点的坐标,根据待定系数法,可得答案.
解答: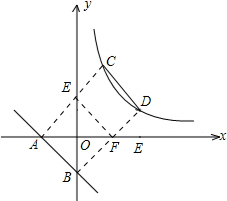 解:如图连接AC,BD,
解:如图连接AC,BD,
当y=0时-2x-2=0,解得x=-1,即A点坐标是(-1,0);
当x=0时,y=-2,即B点坐标是(0,-2).
由平移的性质,得
EF∥AB∥CD,AB=EF=CD.
∠FEO=∠ABO,∠EFO=∠BAO.
在△EOF和△BOA中
,
∴△EOF≌△BOA,(ASA),
∴OE=OB.
E点坐标是(0,2).
由OE=AE,得E是AC的中点,
设E(x,y),由中点的性质,得
=0,
=2,
解得x=1,y=4,即C点坐标是(1,4).
反比例函数y=
(x>0)经过C,
得4=
.
解得k=4.
 解:如图连接AC,BD,
解:如图连接AC,BD,当y=0时-2x-2=0,解得x=-1,即A点坐标是(-1,0);
当x=0时,y=-2,即B点坐标是(0,-2).
由平移的性质,得
EF∥AB∥CD,AB=EF=CD.
∠FEO=∠ABO,∠EFO=∠BAO.
在△EOF和△BOA中
|
∴△EOF≌△BOA,(ASA),
∴OE=OB.
E点坐标是(0,2).
由OE=AE,得E是AC的中点,
设E(x,y),由中点的性质,得
| -1+x |
| 2 |
| 0+y |
| 2 |
解得x=1,y=4,即C点坐标是(1,4).
反比例函数y=
| k |
| x |
得4=
| k |
| 1 |
解得k=4.
点评:本题考查了反比例函数的综合题,利用了平移的性质,全等三角形的判定与性质,线段中点的性质,待定系数法求解析式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
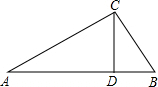 响水县为迎接省卫生文明城市建设,我校把一块形状为直角三角形的废地开辟为植物园,如图所示,∠ACB=90°,AC=80m,BC=60m,若线段CD是一条水渠,且点D在边AB上,已知水渠的造价为100元/米,问点D在距点A多远处时,水渠的造价最低?最低造价是多少?
响水县为迎接省卫生文明城市建设,我校把一块形状为直角三角形的废地开辟为植物园,如图所示,∠ACB=90°,AC=80m,BC=60m,若线段CD是一条水渠,且点D在边AB上,已知水渠的造价为100元/米,问点D在距点A多远处时,水渠的造价最低?最低造价是多少? 如图,在△ABC中,AB、AC的垂直平分线分别交BC于D、E.
如图,在△ABC中,AB、AC的垂直平分线分别交BC于D、E. 在Rt△ABC,∠C=90°,AC=6cm,BC=8cm,点P由点A出发,沿AC方向向点C匀速运动,速度为2cm/s,点Q由AB中点D出发,沿DB向B匀速运动,速度为1cm/s,连接PQ,若设运动时间为t(s)(0<t≤3).
在Rt△ABC,∠C=90°,AC=6cm,BC=8cm,点P由点A出发,沿AC方向向点C匀速运动,速度为2cm/s,点Q由AB中点D出发,沿DB向B匀速运动,速度为1cm/s,连接PQ,若设运动时间为t(s)(0<t≤3).