题目内容
某水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克.经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克.
(1)设每天盈利w元,求出w关于x的函数关系式,并说明每天盈利是否可以达到8000元?
(2)若该商场要保证每天盈利6000元,同时又要使顾客得到实惠,那么每千克应涨价多少元?
(1)设每天盈利w元,求出w关于x的函数关系式,并说明每天盈利是否可以达到8000元?
(2)若该商场要保证每天盈利6000元,同时又要使顾客得到实惠,那么每千克应涨价多少元?
考点:一元二次方程的应用
专题:
分析:(1)设每千克水果应涨价x元,根据总利润=单件利润×件数列出函数关系式即可;
(2)设每千克水果应涨价x元,得出日销售量将减少20x千克,再由盈利额=每千克盈利×日销售量,依题意得方程求解即可.
(2)设每千克水果应涨价x元,得出日销售量将减少20x千克,再由盈利额=每千克盈利×日销售量,依题意得方程求解即可.
解答:解:(1)设每千克水果应涨价x元,
根据题意得:w=(500-20x)(10+x)=-20x2+300x+5000=-20(x-7.5)2+6125,
∵6125<8000,
∴盈利不能达到8000元;
(2)设每千克水果应涨价x元,
依题意得方程:(500-20x)(10+x)=6000,
整理,得x2-15x+50=0,
解这个方程,得x1=5,x2=10.
要使顾客得到实惠,应取x=5.
答:每千克水果应涨价5元.
根据题意得:w=(500-20x)(10+x)=-20x2+300x+5000=-20(x-7.5)2+6125,
∵6125<8000,
∴盈利不能达到8000元;
(2)设每千克水果应涨价x元,
依题意得方程:(500-20x)(10+x)=6000,
整理,得x2-15x+50=0,
解这个方程,得x1=5,x2=10.
要使顾客得到实惠,应取x=5.
答:每千克水果应涨价5元.
点评:考查了一元二次方程的应用,解答此题的关键是熟知此题的等量关系是:盈利额=每千克盈利×日销售量.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
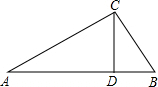 响水县为迎接省卫生文明城市建设,我校把一块形状为直角三角形的废地开辟为植物园,如图所示,∠ACB=90°,AC=80m,BC=60m,若线段CD是一条水渠,且点D在边AB上,已知水渠的造价为100元/米,问点D在距点A多远处时,水渠的造价最低?最低造价是多少?
响水县为迎接省卫生文明城市建设,我校把一块形状为直角三角形的废地开辟为植物园,如图所示,∠ACB=90°,AC=80m,BC=60m,若线段CD是一条水渠,且点D在边AB上,已知水渠的造价为100元/米,问点D在距点A多远处时,水渠的造价最低?最低造价是多少? 一个几何体是由几个相同的立方块搭成的,如图是从上面看的形状图,小正方形
一个几何体是由几个相同的立方块搭成的,如图是从上面看的形状图,小正方形 如图,在△ABC中,AB、AC的垂直平分线分别交BC于D、E.
如图,在△ABC中,AB、AC的垂直平分线分别交BC于D、E.