Question

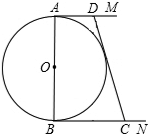如图，⊙0的直径AB=2，AM和BN是它的两条切线，且AD+BC=CD，连OD，OC，
（1）求证：AM∥BN；
（2）求证：DC是⊙O切线；
（3）设AD=x，求四边形ABCD的面积S与x的关系式．

Answer 1

考点：切线的判定与性质

专题：

分析：（1）根据切线的性质证得AB⊥AD，AB⊥BC，根据平行线的判定即可证得；
（2）连接OD、OC，作OE⊥CD于E，根据S_△DOC+S_△AOD+S_△BOC=S_梯形即可证得OE=OA，从而证得DC是⊙O切线；
（3）作DF⊥BN交BC于F，证得四边形ABFD是矩形，从而得出BF=AD=x，DF=AB=2，设BC=y，根据勾股定理求得y与x的关系式，然后根据梯形的面积公式即可求得．

解答：（1）证明：∵AM和BN是⊙O的两条切线，
∴AB⊥AD，AB⊥BC，
∴AM∥BN．
（2）证明：连接OD、OC，作OE⊥CD于E，
∵S_△DOC+S_△AOD+S_△BOC=S_梯形，
S_△DOC=

1

2

CD•OE=

1

2

（AD+BC）•OE，
S_△AOD=

1

2

AD•OA，
S_△BOC=

1

2

BC•OB=

1

2

BC•OA，
S_梯形=

1

2

（AD+BC）•AB=（AD+BC）•OA，
∴（AD+BC）•OA=

1

2

（AD+BC）•OE+

1

2

AD•OA+

1

2

BC•OA，
∴OA=

1

2

OE+

1

2

OA，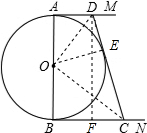
∴OE=OA，
∴DC是⊙O切线；
（3）解：作DF⊥BN交BC于F，
∵AB⊥AM，AB⊥BN．
又∵DF⊥BN，
∴∠BAD=∠ABC=∠BFD=90°，
∴四边形ABFD是矩形，
∴BF=AD=x，DF=AB=2，
设BC=y，
∴FC=BC-BF=y-x；
∵AM和BN是⊙O的两条切线，DE切⊙O于E，
∴DE=DA=x CE=CB=y，
则DC=DE+CE=x+y，
在Rt△DFC中，由勾股定理得：（x+y）²=（x-y）²+2²，
整理得：y=

1

x

，
∴S=

1

2

（AD+BC）•AB=

1

2

（x+

1

x

）×2=x+

1

x

，
即S=x+

1

x

．

点评：此题考查了切线的性质和判定，勾股定理，矩形的性质的应用，注意：数形结合思想和方程思想的应用，解此题的关键是能正确作出辅助线．